Nimble Model Building

This software supports nimble model building with functions to set up, solve, and analyze dynamical systems models for mosquito ecology and mosquito-borne pathogen transmission formulated as dynamical systems in continuous or discrete time. The systems are naturally modular: an intermediate step in developing a model for ramp.xds is to rewrite the equations using Modular Forms.

The mathematical framework and software have a modular design developed around an algorithm to model mosquito blood feeding on vertebrate hosts and parasite / pathogen transmission, including patch-based spatial dynamics within a defined geographical domain. The blood feeding algorithm provides a rigorous computational interface linking dynamical components describing parasite/pathogen linking infection dynamics in mosquito and vertebrate host populations. It guarantees mathematical consistency in computing blood feeding rates and habits and in allocating bites and blood meals with heterogeneous vertebrate host population densities, including models with dynamically changing availability of host populations or other vertebrate animals.

The framework and software also support spatial models of mosquito ecology through an algorithm that describes egg laying by adult mosquitoes in aquatic habitats and emergence of adult mosquitoes. The egg laying algorithm provides a rigorous interface linking dynamical components describing adult mosquito populations in a set of spatial patches and immature aquatic mosquito populations in a structured set of aquatic habitats.

Modularity

Dynamical systems models for malaria and other mosquito-borne pathogens (MBPs) are naturally modular. Transmission dynamics involve infection dynamics in populations of two different species of hosts: a mosquito host, and a human or other vertebrate animal host. Parasite / pathogen transmission occurs through blood feeding. The modular nature of these systems can be emphasized by rewriting the equations using modular forms

Mosquito population density is a parameter in the Ross-Macdonald model. Many dynamical systems describing transmission dynamics and control for malaria and other MBPs include equations describing mosquito ecology and population dynamics: volant adult and aquatic immature mosquito sub-populations connected through egg-laying and emergence. The equations describing these dynamics can be organized around blood feeding (for transmission) or egg-laying and emergence (for mosquito ecology).

In simple models, the assumptions about

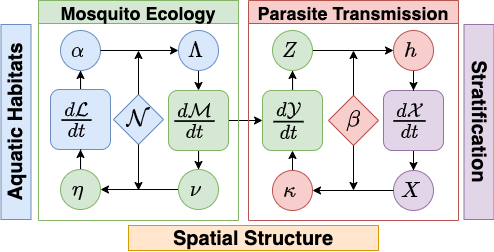
$Figure 1 A diagram of the core components in dynamical systems models of malaria: \cal L$

Figure 1 A diagram of the core components in dynamical systems models of malaria: $\cal L$

Dynamical systems for malaria and other MBPs have a broad set of other features: spatial dynamics; human/host demography; heterogeneous transmission; various forms of vector control; health interventions; mosquito resource dynamics; malaria importation; and exogenous forcing by weather.

Modularity

Ross

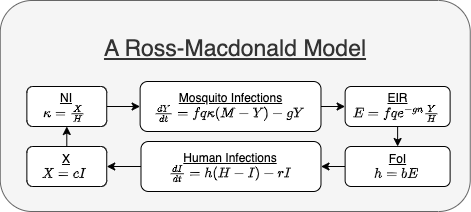
In ramp.xds, the equations are solved by computing the terms and the derivatives separately.

Transmission(t,y,pars) computes three terms required to compute parasite transmission during blood feeding. These are stored in the main model object pars:
- pars$beta - a function that allocates infective bites to human strata. In this case, $\beta = 1/H$
- pars$NI - a function $F_X$ computes the effective density. In this case, $F_X$ returns $cI$
- pars$fqZ - a function $F_fqZ$ computes infective biting density
- pars$EIR - the daily EIR is $\beta \cdot fqZ$
- pars$FoI - the daily FoI is $F_h(EIR, b, pars$ Xpar)$
Exposure(t, y, pars) computes the FoI from the EIR under a model of exposure and stores it as pars$FoI

So instead of developing models like RMv1, we have implemented the code in the syle of RMv2:

RMv2 <- function(t, y, pars) {
  with(pars,{
      pars = Transmission(t, y, pars)
      pars = Exposure(t, y, pars)
      dX = dXdt(t, y, pars) 
      dY = dMYZdt(t, y, pars) 
      return(list(dX, dY))
  })
}

Model building in ramp.xds

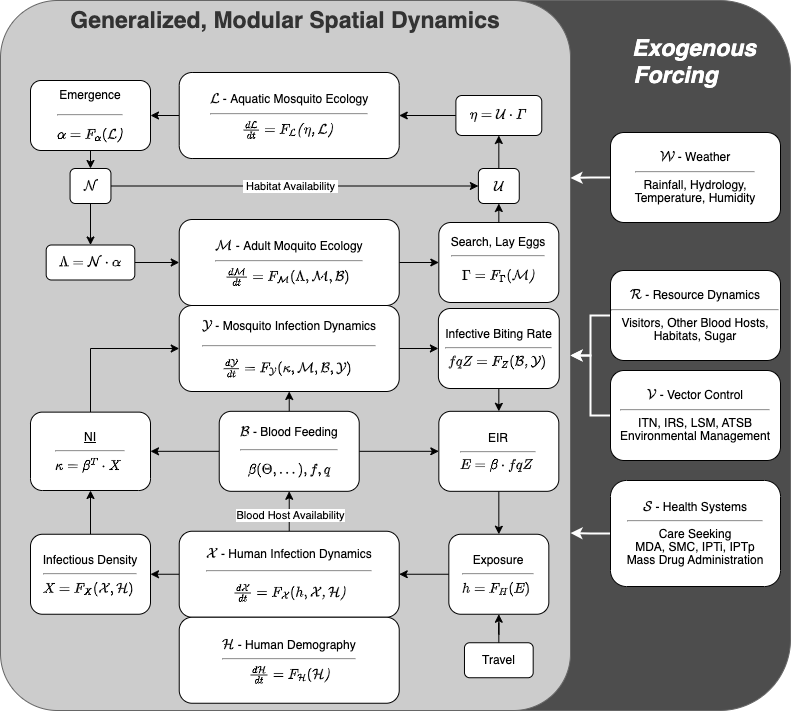
Models for mosquito borne pathogen transmission systems are naturally modular, structured by vector life stage, host population strata, and by the spatial locations (patches) at which transmission occurs (see figure below).

Models in the ramp.xds framework are constructed from 3 dynamical components:

$\mathcal M$ : adult mosquitoes, whose dynamics are described by $d\mathcal{M}/dt$
$\mathcal{L}$ : aquatic (immature) mosquitoes, whose dynamics are described by $d\mathcal{L}/dt$
$\mathcal{X}$ : human population, whose dynamics are described by $d\mathcal{X}/dt$

The combined state from these 3 components is the entire state of the dynamical model, and their combined dynamics described by their differential equations represents the full endogenous dynamics of the system. In addition there are 2 more components which do not directly contribute to the state of the model, but instead modify parameters and compute intermediate quantities to represent external influences on the system. These are:

Exogenous forcing: weather, climate, unmodeled populations
Vector control: public health and mosquito control interventions which affect the dynamical components

There are also functions which handle the exchange of information (flows) between the dynamical components and which couple their dynamics. Bloodfeeding is the process by which adult mosquitoes seek out and feed on blood hosts, and results in the quantities $EIR$ (entomological inoculation rate) and $\kappa$ , the net infectiousness of humans to mosquitoes, which couple the dynamics of $\mathcal{M}$ and $\mathcal{X}$ . Likewise emergence of new adults from aquatic habitats and egg laying by adults into habitats couples $\mathcal{M}$ and $\mathcal{L}$ .

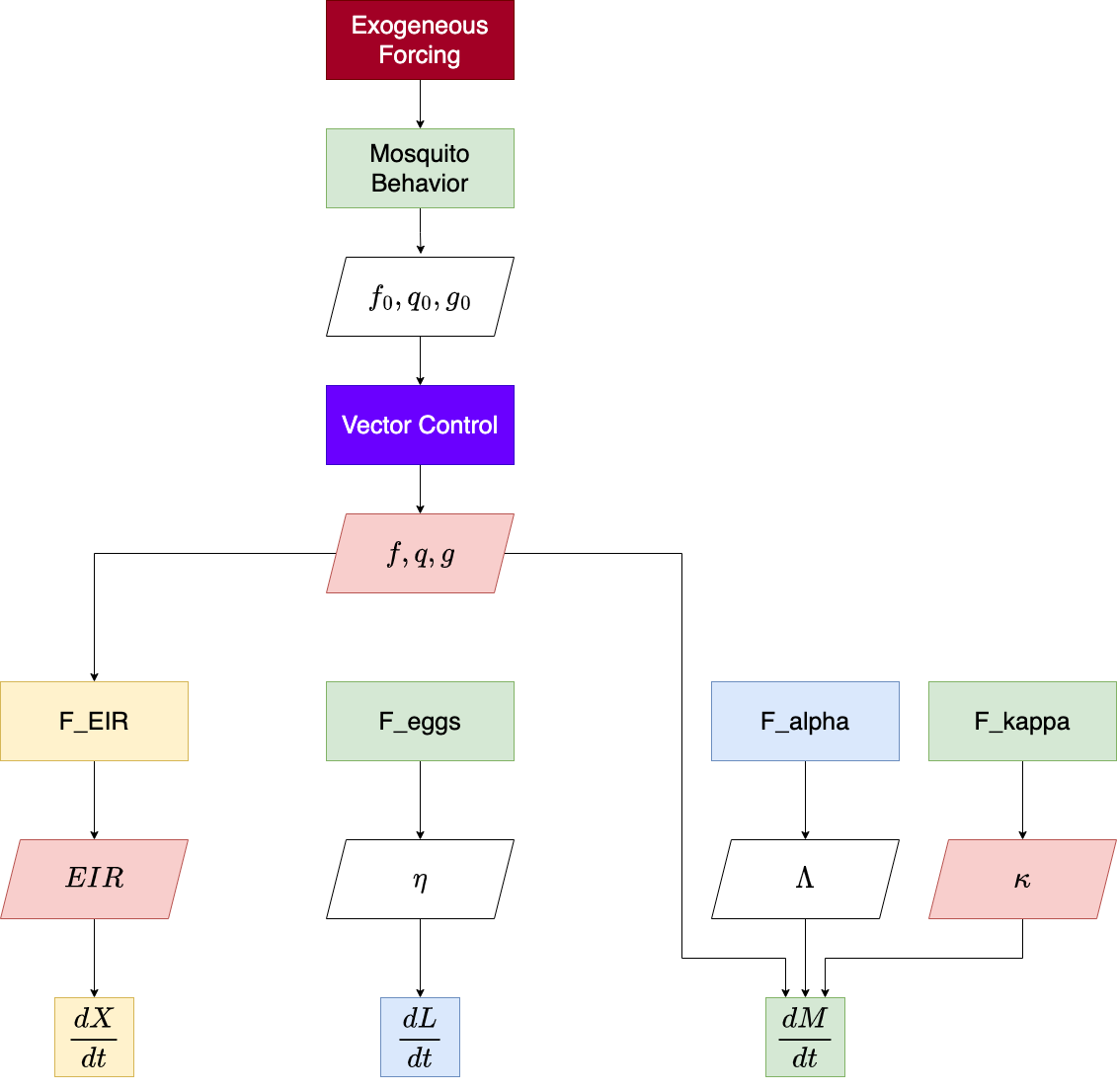
The function ramp.xds::xde_derivatives compute the necessary quantities and returns a vector of derivatives of all state variables which can be used to solve trajectories from a model in ramp.xds. The program flow within this function is summarized by this diagram:

For more information, please read our research article describing the theory behind the model.

Modular Dynamical Systems & Computatation for Malaria & Other Mosquito-Transmitted Pathogens

Modularity

Model building in ramp.xds