Modular Forms for Disease Dynamics • ramp.xds

A modular form is a stylized way of writing down a dynamical systems that emphasizes the structure of the underlying process. The modular structure of ramp.xds can be understood through the use of these forms. The forms we describe here rewrite models so that they closely resemble their implementation in ramp.xds, which makes it possible to relate written equations and computed code.

A Standard Form

A mathematical framework for building modular models of malaria dynamics and control (and other mosquito-borne pathogens) was described in Spatial Dynamics of Malaria Transmission, and that framework has been implemented in ramp.xds.

There is no standard form for writing down systems of differential equations, but many forms are used, depending on context. For comparison, we writing down a system of equations that does not emphasize the modularity, or not a modular form.

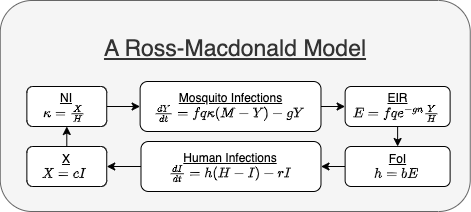
To illustrate the modular form, we start with the Ross-Macdonald-style model in Box 1.

Box 1: A Ross-Macdonald Model

Let the dependent variable $I(t)$ denote the density of infected humans, and the parameter $H$ the density of all humans
Let the dependent variable $Y(t)$ denote the density of infected mosquitoes, and the parameter $M$ the density of all mosquitoes
Let $b$ denote the fraction of bites by infective mosquitoes that infect a human, and let $r$ denote the rate that infections clear
Let $c$ denote the fraction of blood meals on infectious humans infect a mosquito, and let $g$ denote the mosquito death rate
Let $f$ denote the overall blood feeding rate, and $q$ the human fraction
Let $\tau$ denote the EIP.

In this set of equations, we ignore the delay for sporogony, but we count the mortality, so infections occur at the rate $b e^{-g \tau} fqY/H.$ We assume that the daily FoI is linearly proportional to the daily EIR, consistent with a Poisson model for exposure, so $h = bE.$

$\begin{array}{rl} dI/dt &= b e^{-gn}fq \frac YH (H-I) - r I \\ dY/dt &= fq c \frac IH (M-Y) - g Y \end{array}$

…in Modular Form

We illustrate by writing a Ross-Macdonald model in its modular form (Figure 1). In the modular form, we identify the terms in one equation that depend on the other variable. First, we focus on the equation describing human infection dynamics. We note that it depends on a term involving the variable $Y.$ The term is epidemiologically meaningful – it is called the force of infection (FoI). We let $h$ denote the FoI: $h=b e^{-gn}fq \frac YH,$

and now we can rewrite the equation

$dI/dt = h (H-I) - r I$

Next, we isolate the equation describing mosquito infection dynamics, we note that it depends on a term that we will call the net infectiousness (NI).

$\kappa = \frac XH$

The term $X = c I$ is the density of infected humans, weighted by their infectiousness.

We note that $fq\kappa$ is the FoI for mosquito infections, and now we can rewrite the equation for mosquitoes:

$dY/dt = fq\kappa (M-Y) - g Y$

Since we also want to make this model extensible, we want to draw attention to the term $h.$ We note that the number of infective bites, per human, per day – called the daily entomological inoculation rate (EIR) – is

$E = f q e^{-g\tau} \frac YH$

We assume that exposure is Poisson distributed:

$h = b E$

We emphasize that this is the same set

Figure 1 - Diagram of a Ross-Macdonald model in Box 1, rewritten in a modular form.

Computation

To solve these equations, we need to write functions that compute the derivatives. We are using the R package deSolve. A properly formed derivative function implementing the

RMv1 <- function(t, y, pars) {
  with(pars,{
      eir = exp(-g*n)*Y/H
      foi = b*eir
      kappa = c*I/H
      dX = foi*(H-I) - r*I
      dY = a*kappa*(M-Y) - g*Y 
      return(list(dX, dY))
  })
}

Full Modularity

For a longer discussion of modularity, see the vignette modularity