Skip to contents

Getting Started

Source: vignettes/GettingStarted.Rmd
GettingStarted.Rmd

Next: Basic Setup.

Additional documentation is available in the SimBA Project website.

ramp.xds was developed to reduce the costs of building, solving, analyzing, and using models describing the epidemiology, transmission dynamics and control of malaria and other mosquito-transmitted pathogens. This vignette gives a demonstration and a basic introduction.

Installation

The software was developed in RStudio. To download the R package, run these commands:

library(devtools)
devtools::install_github("dd-harp/ramp.xds")

Then load ramp.xds:

Additional modules and functionality are available in companion R-packages, including ramp.library, ramp.control, ramp.forcing, and ramp.demog. For more information, see the SimBA Project website.

Demo

ramp.xds makes it easy to build and use models for the transmission dynamics and control of malaria or other mosquito-borne pathogens. Model building in ramp.xds starts with a function called xds_setup(). All arguments in xds_setup() are assigned default values, so calling xds_setup() with no arguments returns a fully configured model with all the default settings.

model <- xds_setup()

The object model returned by xds_setup() is called a xds model object: it is a fully defined model that can be solved by xds_solve().

Defaults

The arguments are stored and can be easily retrieved. The name of the module for human / host infection and immune dynamics is stored as Xname. The default module is the SIS compartmental model:

model$Xname
## [1] "SIS"

SIS was set up with default parameter values, that can be viewed with the function get_XH_obj:

## $b
## [1] 0.55
## 
## $c
## [1] 0.15
## 
## $r
## [1] 0.005555556

Functions like get_XH_pars are designed to help users get to know the model oject. In this case, the parameters are stored as model$Xpar[[i]], for the \(i^{th}\) species. Knowing the names, the parameters can then be viewed (or changed):

model$XH_obj[[1]]$r
## [1] 0.005555556

To make it easy to change parameters, we also wrote the change_XH_pars by passing the new values to be changed in a named list.

model <- change_XH_pars(model, 1, list(r=1/150))
get_XH_pars(model)$r
## [1] 0.006666667

Similarly, initial values were assigned default values at setup. In ramp.xds, human/host demography is treated as a distinct process, so the intial values for :

get_XH_inits(model, 1)
## $H
## [1] 1000
## 
## $I
## [1] 1

The default parameters and initial values can be over-written at setup by passing options = list(...) with different values. Since xds_setup calls functions to set up several model objects, each component has its own options name. For the XH component, setup options for the XH component are passed in XHoptions:

Xo = list(b=1/150, c=0.2, b=0.6, I=2)
model1 <- xds_setup(XHoptions = Xo)
get_XH_pars(model1)
## $b
## [1] 0.006666667
## 
## $c
## [1] 0.2
## 
## $r
## [1] 0.005555556

In the SIS model, we set \(H=S+I,\) so the software computes \(dH/dt\) and \(dI/dt\) and sets \(S=H-I.\) By policy, the software computes the total population size, \(H,\) dynamically and treats it differently. This is because plays an important role in setting up the Blood Feeding interface, so it is not possible to set \(S.\) Instead, \(S\) is computed after solving and parsing.

get_XH_inits(model1)
## $H
## [1] 1000
## 
## $I
## [1] 2

To change the human population density, use the change_H function.

model1 <- change_H(1004, model1)
get_XH_inits(model1)
## $H
## [1] 1000
## 
## $I
## [1] 2

The module for adult mosquito ecology and infection dynamics is called MYname. The default module is Macdonald’s model:

model$MYname
## [1] "macdonald"

The design pattern is followed: once again, parameters can be viewed with get_MY_pars and the method for setting parameter values by passing a named list of values to MYoptions in xds_setup() or changing the parameter values by passing new values by name in a list to change_MY_pars.

The name of the default module for aquatic mosquito ecology is called Lname. The default module is the trivial module:

model$Lname
## [1] "trivial"

For the trivial module, arguments passed at the command line configure functions that pass values to other dynamical components.

The design pattern is followed: parameters can be viewed with get_L_pars and the method for setting parameter values by passing a named list of values to Loptions in xds_setup(). After setup, the change_L_pars works in the same way as the other change_ functions.

Solving

After setting up, model has an empty placeholder for outputs:

model$outputs 
## list()

Calling xds_solve(model) returns solutions to the initial value problem(s): xds_solve calls deSolve, and the values of the dependent variables at a set of time points are attached as model$outputs.

There are three ways to pass the argument time to deSolve: first, xds_solve can set up a vector of time points seq(0, Tmax, by = dt) that are configurable with the arguments Tmax and dt; second, if no arguments are passed for time, then it uses the defaults Tmax=365 and dt=1; third, deSolve will use the optional argument times if it is supplied. All four of the following do the same thing:

model <- xds_solve(model, times=0:365) 
model <- xds_solve(model, times=0:365, Tmax=730, dt=5) 
model <- xds_solve(model, Tmax=365, dt=1) 
model <- xds_solve(model)

Internally, these are handled by the function make_times_xde for systems of differential equations, and make_times_dts for discrete time systems.

Note xds_solve requires an xds model object and that it returns an xds model object. In this case, the function passes model and the return value replaces model. Before xds_solve, model$outputs was an empty list. After solving, the outputs are stored as model$outputs:

names(model$outputs)
## [1] "deout"  "time"   "last_y" "orbits"

The outputs from solving a system of equations include:

  • deout – the raw (unparsed) outputs
  • time – the time points where dependent variables were computed
  • last_y – the last state of the system
  • orbits – solutions with the values of the dependent variables and terms parsed by name, accessible separately for each dynamical component

Note that the time holds the default values of the independent variable time where we solved the initial value problem for the dependent variables.

head(model$outputs$time, 5)
## [1] 0 1 2 3 4
tail(model$outputs$time, 3)
## [1] 363 364 365

When xds_solve is called, the xds model object it returns has replaced any old values. If nothing has changed, then the outputs will be identical.

On the other hand, if anything has changed, any old outputs will get replaced. If the outputs need to be saved for future analyses, the user will probably have to write a wrapper function that extracts and saves it.

Parsing

To make it easy to deal with the outputs, the dependent variables are parsed and returned in named lists. xde_solve() also computes some standard terms that are likely to be of interest.

Functions like get_EIR() make it easy to examine or save a set of standard outputs without delving into the details.

head(get_EIR(model), 3)
##              [,1]
## [1,] 0.0002850000
## [2,] 0.0002622311
## [3,] 0.0002412851

Visualizing

ramp.xds includes functions to plot standard outputs:

  • xds_plot_X plots the density of infected individuals

  • xds_plot_M plots the density of adult female mosquitoes in each patch

  • xds_plot_Y plots the density of infected adult female mosquitoes in each patch

  • xds_plot_Z plots the density of infectious adult female mosquitoes in each patch

  • xds_plot_PR plots the true prevalence of infection in the human / host population

  • xds_plot_EIR plots the EIR for each one of the human / host population strata

par(mfrow = c(2,2))
xds_plot_X(model)
xds_plot_M(model)
xds_plot_Y(model, add=T)
xds_plot_Z(model, add=T)
xds_plot_PR(model)
xds_plot_EIR(model)
**Figure 1:** Plotting standard outputs

Figure 1: Plotting standard outputs

Trivial Models and Trace Functions

The software was designed to be fully modular, so that any module for one dynamical component can be replaced with another. The models included in ramp.xds are just enough to illustrate its the features ensure that the software is working as it should.

A basic requirement for full modularity is that every dynamical component must include a trivial module. In the trivial module, no variables are defined, but the dynamical terms needed by related dynamical components are passed by a configurable trace function with a generic form:

mean*F_season(t)*F_trend(t)

The default for the aquatic mosquito dynamical component is the trivial module, where the mean is is called Lambda.

It is easy to change the trace function. First, we define F_season and change the mean value of Lambda. The generic format for seasonal functions is F_season(t, phase, season_opts), where phase sets the phase (time of year), and season_opts is a set of configurable parameter values:

 F_sp = function(t){(1+sin(2*pi*t/365))}

Having defined F_sp, we now configure a list of options:

Lo = list(
       Lambda=500, 
       F_season=F_sp
      )

We use the first model as a template for the new model, but we assign the return value a new name model_1 so that the original one still exists:

model_1 <- setup_L_obj("trivial", model, 1, options=Lo)

We want to change the initial values of model_1. Since model_1 was copied from model, the last values from solving it are available, and we can use a function last_to_inits to set the initial values.

model_1 <- last_to_inits(model_1)

Now, we solve it over a three year period

model_1 <- xds_solve(model_1, Tmax=365*3, dt=5)

and plot the results.

par(mfrow = c(1,2))
xds_plot_X(model_1)
xds_plot_M(model_1)
xds_plot_Y(model_1, add=T)
xds_plot_Z(model_1, add=T)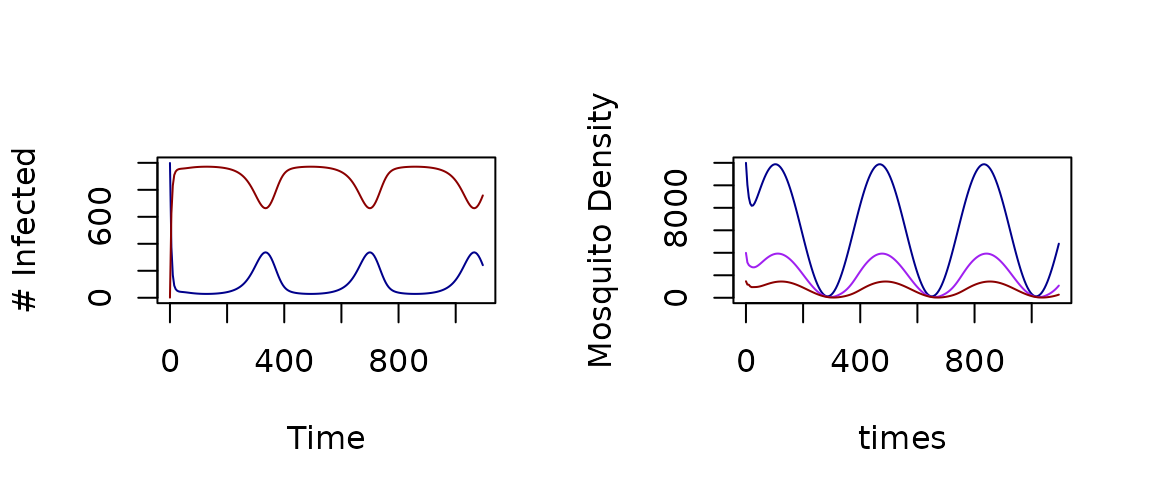
**Figure 2:** Outputs with Seasonal Forced Emergence using a Trace Function

Figure 2: Outputs with Seasonal Forced Emergence using a Trace Function