Basic Competition Aquatic Mosquito Model • exDE

The basic competition aquatic mosquito model fulfills the generic interface of the aquatic mosquito component. It has a single compartment “larvae” for each aquatic habitat, and mosquitoes in that aquatic habitat suffer density-independent and dependent mortality, and mature at some rate \(\psi\).

Differential Equations

Given \(\Lambda\) and some egg laying rate from the adult mosquito population we could formulate and solve a dynamical model of aquatic mosquitoes to give that emergence rate. However, in the example here we will simply use a trace-based (forced) emergence model, so that \(\Lambda\) completely specifies the aquatic mosquitoes.

The simplest model of aquatic (immature) mosquito dynamics with negative feedback (density dependence) is:

\[ \dot{L} = \eta - (\psi+\phi+\theta L)L \]

Because the equations allow the number of larval habitats \(l\) to differ from \(p\), in general the emergence rate is given by:

\[ \Lambda = \mathcal{N}\cdot \alpha \]

Where \(\mathcal{N}\) is a \(p\times l\) matrix and \(\alpha\) is a length \(l\) column vector given as:

\[ \alpha = \psi L \]

Equilibrium solutions

In general, if we know the value of \(\Lambda\) at equilibrium we can solve for \(L\) directly by using the above two equations. Then we can consider \(\theta\), the strength of density dependence to be unknown and solve such that:

\[ \theta = (\eta - \psi L - \phi L) / L^2 \]

Example

library(exDE)
library(deSolve)
library(data.table)
library(ggplot2)

The long way

Here we run a simple example with 3 aquatic habitats at equilibrium. We use exDE::make_parameters_L_basic to set up parameters. Please note that this only runs the aquatic mosquito component and that most users should read our fully worked example to run a full simulation.

nHabitats <- 3
alpha <- c(10, 50, 20)
eta <- c(250, 500, 170)
psi <- 1/10
phi <- 1/12
L <- alpha/psi
theta <- (eta - psi*L - phi*L)/(L^2)

params <- make_parameters_xde() 
params$nHabitats = nHabitats
params$eggs_laid = list() 
params$eggs_laid[[1]] = eta 
F_eta = function(t, pars){
  pars$eggs_laid[[1]]
}

params = make_parameters_L_basic(pars = params, psi = psi, phi = phi, theta = theta)
params = make_inits_L_basic(params, L0=L)

params = make_indices(params)

xDE_aquatic = function(t, y, pars, F_eta) {
  pars$eggs_laid[[1]] <- F_eta(t, pars)
  dL <- dLdt(t, y, pars, 1)
  return(list(c(dL)))
}

y0 <- get_inits(params) 

out <- deSolve::ode(y = y0, times = 0:50, xDE_aquatic, parms = params, method = 'lsoda', F_eta = F_eta) 
out1 <- out

colnames(out)[params$L_ix+1] <- paste0('L_', 1:params$nHabitats)

out <- as.data.table(out)
out <- melt(out, id.vars = 'time')
out[, c("Component", "Patch") := tstrsplit(variable, '_', fixed = TRUE)]
out[, variable := NULL]

ggplot(data = out, mapping = aes(x = time, y = value, color = Patch)) +
  geom_line() +
  theme_bw()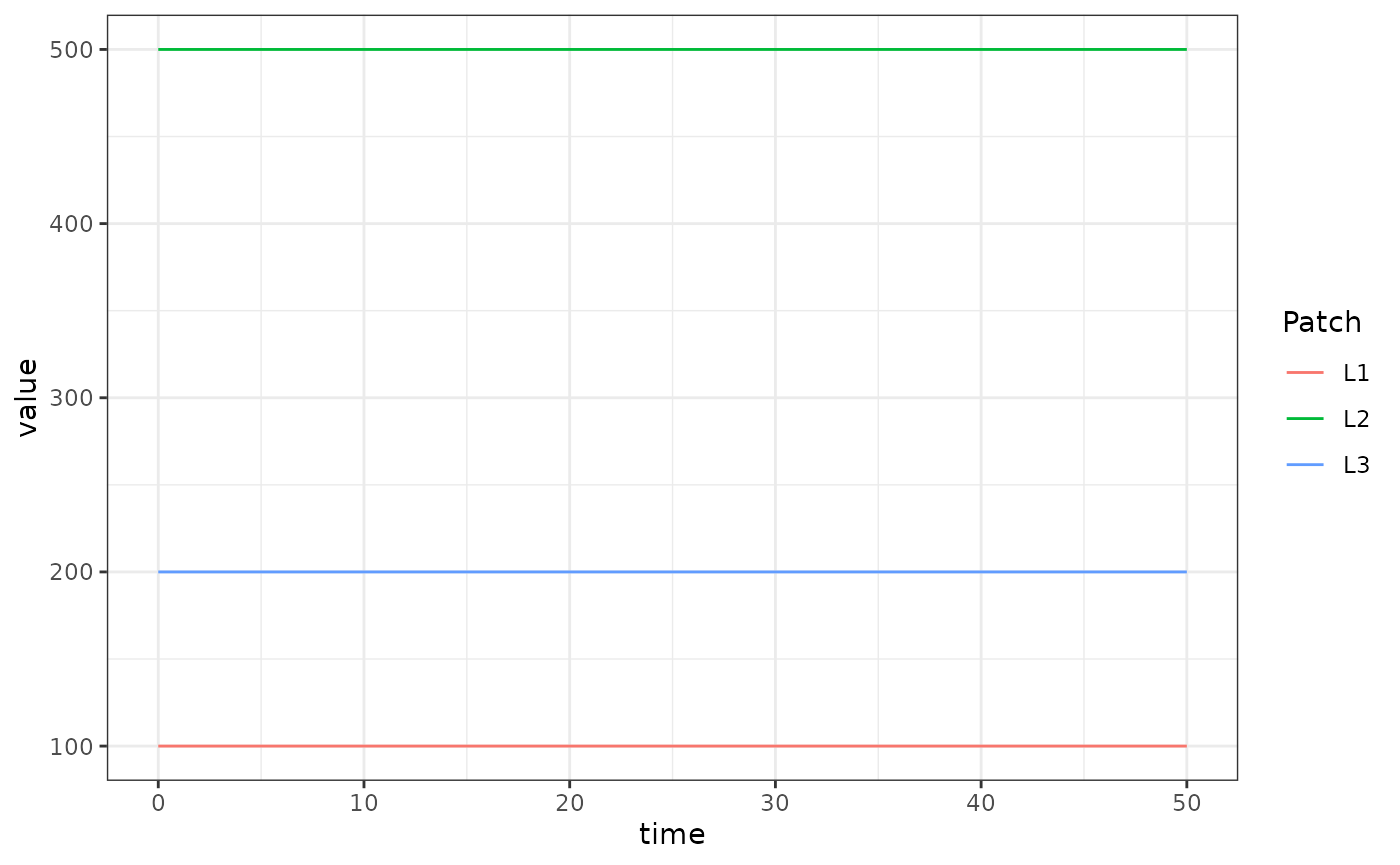

Using Setup

The function xde_setup_aquatic sets up a model that includes only aquatic dynamics, and it is solved using xde_solve.aqua. The setup functions are simpler than xde_setup and come with constrained choices. The user can configure any aquatic model (trace wouldn’t make much sense), and it uses Gtrace to force egg laying.

We configure the aquatic model: Lo is a list with the parameter values attached.

Lo = list(
  psi = 1/10, 
  phi = 1/12
)
alpha = c(10, 50, 20)
Lo$L0 = with(Lo, alpha/psi) 
Lo$theta = with(Lo, (eta - psi*L0 - phi*L0)/(L0^2))

We use the MYZ model Gtrace to configure egg laying.

Mo = list(Gm = c(250, 500, 170))

xde_setup_aquatic(nHabitats = 3, Lname = "basic", Lopts = Lo, MYZopts = Mo) -> aqbasic
xde_solve(aqbasic, Tmax=50, dt=1)$output$orbits$deout -> out2
sum(abs(out1-out2)) == 0
#> [1] TRUE