Make an exponential function for weight by distance

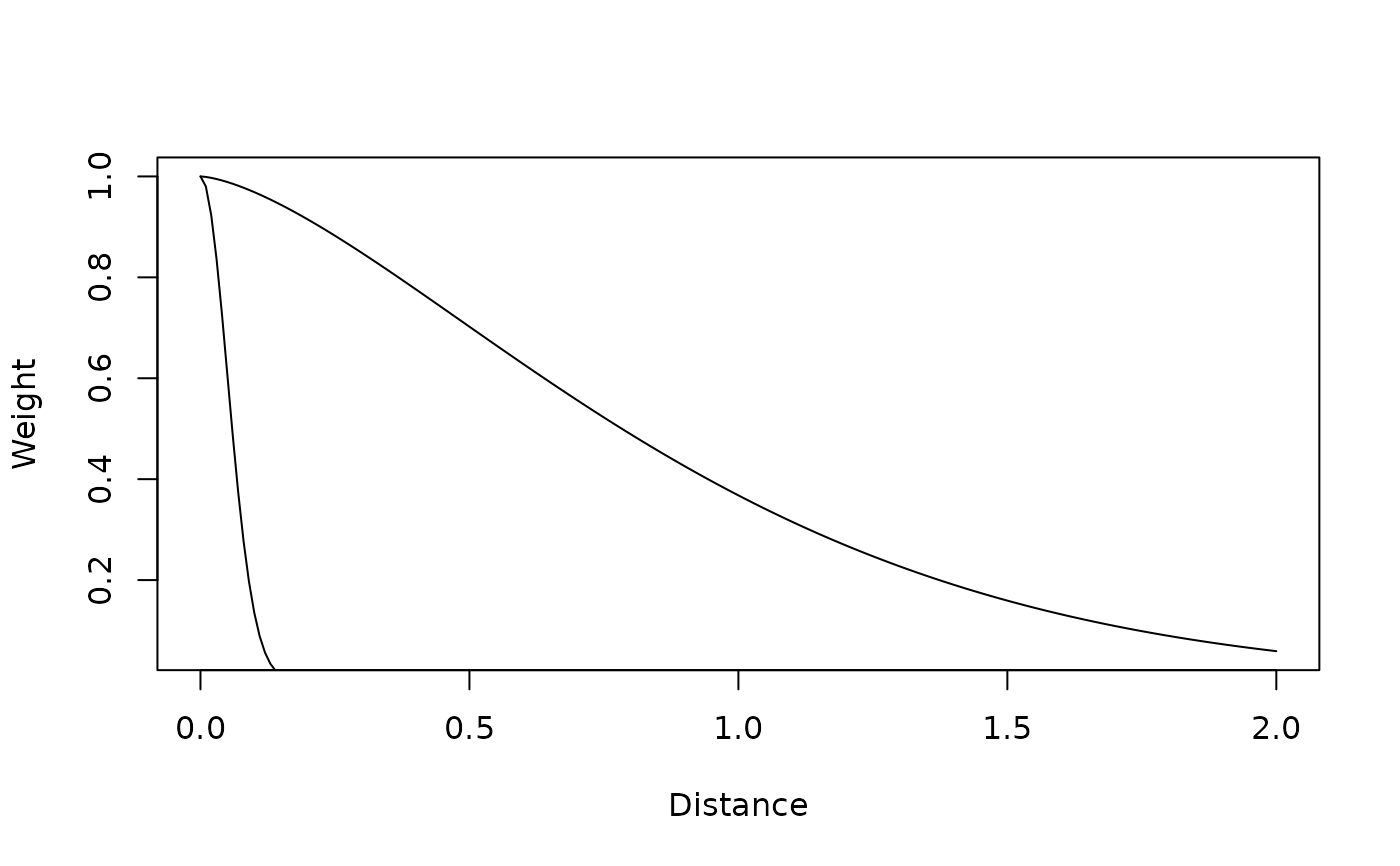
This returns a function of the form $$F_w (d, \omega=1) = \omega_j e^{-k \left( \frac{d_{i,j}}{s}\right)^\gamma}$$ where \(s\) and \(\gamma\) are shape parameters, \(k\) is the rate parameter, and \(\omega\) is a weight.

In effect, \(s\) is the location of a shoulder, and for \(\gamma>1\), the decay is slower for \(d<s\).

The function returned accepts \(\omega\) as an optional argument so that it can be passed at the time of simulation.

By default, the function returns scaled values – the maximum is 1.