Adult Mosquitoes - BQS

Point Sets

We define this class of micro-simulation models on point sets representing the locations of resources: haunts where mosquitoes rest and where a mosquito might find and feed on a vertebrate host; and aquatic habitats where mosquitoes could find aquatic habitats and lay eggs.

• Let $\left\{ b \right\}$ denote the point set where blood feeding could occur;

• Let $\left\{ q \right\}$ denote the point set where egg laying could occur;

• Let $\left\{ s \right\}$ denote the point set where sugar feeding could occur;

Dispersal

Movement among point sets is modeled using matrices that describe where mosquitoes move each time step. The proportion moving from a point in one set to another, from $x\in \left\{ x \right\}$ to $y \in \left\{ y \right\}$, is described by a matrix $\Psi_{y\leftarrow x}$ or equivalently $\Psi_{yx}$. Similarly, the proportion moving from a point in one set to a point in the other is $\Psi_{xx}$.

• Note that the diagonal of $\Psi_{x\leftarrow x}$ is the probability of staying.

• Mortality while searching is referenced to the source point, and it is not part of the dispersal matrices.

• We assume that every surviving mosquito ends up somewhere. Since there are a finite number of destinations, each column is a probability mass function (PMF).

Searching for Blood

• Let $\Psi_{b \leftarrow q}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ b \right\}$ starting from each point in $\left\{ q \right\}$.

• Let $\Psi_{b \leftarrow b}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ b \right\}$ starting from each point in $\left\{ b \right\}$.

• Let $\Psi_{b \leftarrow s}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ b \right\}$ starting from each point in $\left\{ s \right\}$.

Searching for Aquatic Habitats

• Let $\Psi_{q \leftarrow b}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ q \right\}$ starting from each point in $\left\{ b \right\}$.

• Let $\Psi_{q \leftarrow q}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ q \right\}$ starting from each point in $\left\{ q \right\}$.

• Let $\Psi_{q \leftarrow s}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ q \right\}$ starting from each point in $\left\{ s \right\}$.

Searching for Sugar

• Let $\Psi_{s \leftarrow b}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ s \right\}$ starting from each point in $\left\{ b \right\}$.

• Let $\Psi_{s \leftarrow q}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ s \right\}$ starting from each point in $\left\{ q \right\}$.

• Let $\Psi_{s \leftarrow s}$ denote a matrix describing the location where mosquitoes end their flights in $\left\{ s \right\}$ starting from each point in $\left\{ s \right\}$.

Variables & Terms

In the simulation models, the number of adult mosquitoes emerging from each aquatic habitat on each day is a vector denoted $\Lambda_t$ that can be either passed as a parameter or simulated using a population dynamic model for aquatic immature population dynamics. Adult mosquitoes are located at one of these points at each point in time (, one day), represented as a set of vectors: $B_t$, the number seeking blood at haunts; or $Q_t$, the number attempting to lay eggs at habitats.

Emerging Adults

• Let $\Lambda_t$ denote the number of recently emerged mosquitoes at $\left\{ q \right\}$

• Note that $\Lambda_t$ can be passed as a parameter, or it could be computed from a model for aquatic mosquito dynamics.

Adults in Behavioral States

• Let $B_t$ denote the number of blood feeding mosquitoes at $\left\{ b \right\}$

• Let $Q_t$ denote the number of egg laying mosquitoes at $\left\{ q \right\}$

• Let $S_t$ denote the number of sugar feeding mosquitoes at $\left\{ s \right\}$

Parameters

Mosquito bionomics can depend on both behavioral state and location, including daily survival and daily blood feeding or egg laying success. Note that survival is linked to the point where the search started, but foraging success is linked to the point where the mosquito ends up after moving in a time step.

Survival:

• Let $p_b$ denote the probability of surviving for a mosquito at $\left\{ b \right\}$ at time $t$

• Let $p_q$ denote the probability of surviving for a mosquito at $\left\{ q \right\}$ at time $t$

• Let $p_s$ denote the probability of surviving for a mosquito at $\left\{ s \right\}$ at time $t$

Foraging Success:

• Let $\psi_b$ denote the probability of blood feeding for a mosquito at $\left\{ b \right\}$ at time $t$ and let $\hat \psi_b = 1-\psi_b$

• Let $\psi_q$ denote the probability of laying eggs for a mosquito at $\left\{ q \right\}$ at time $t$ and let $\hat \psi_q = 1-\psi_q$

• Let $\psi_s$ denote the probability of sugar feeding for a mosquito at $\left\{ s \right\}$ at time $t$ and let $\hat \psi_s = 1-\psi_s$

State Transitions

In the models with sugar feeding, we to describe the frequency of switching to sugar feeding from other states. Each day, some fraction of mosquitoes switch to a sugar feeding state from various points in the feeding cycle (Figure 1):

• a switch to sugar feeding occurs in a fraction of recently emerged mosquitoes, $\sigma_\Lambda$;

• switch to sugar feeding occurs after egg laying, $\sigma_f$;

• a fraction of egg laying mosquitoes switches to sugar feeding after a failed egg laying attempt, $\sigma_q$. We implicitly assume that the eggs in each batch are lost.

• a fraction of blood feeding mosquitoes switches to sugar feeding after a failed flood feeding attempt, $\sigma_b$.

We assume that all mosquitoes revert to blood feeding after sugar feeding, implying that the mosquito resorbed the eggs. We also assume that mosquitoes would never attempt to sugar feed after a blood meal, but that they would instead always attempt to lay eggs at least once (Fig. 1).

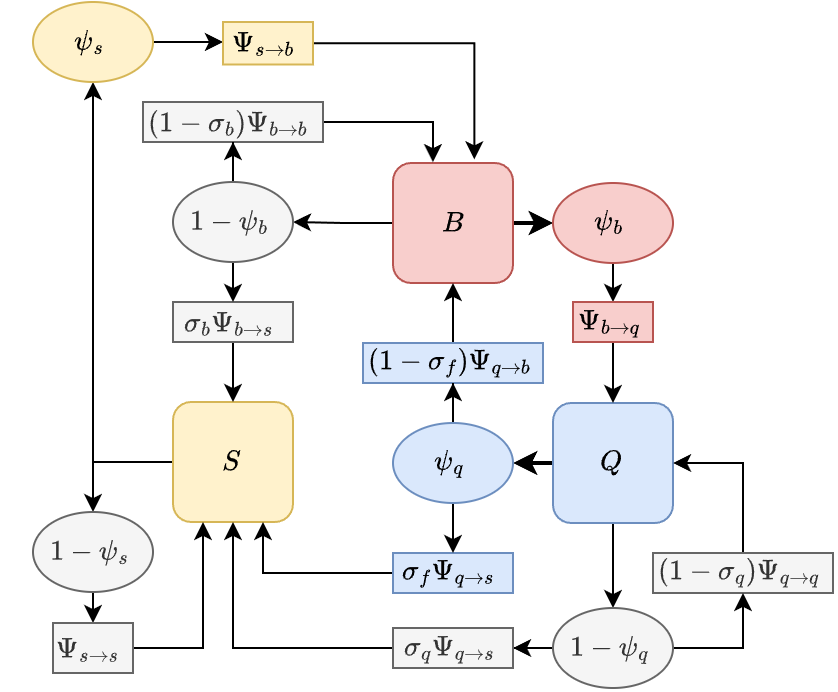
Figure 1 - A diagram of the BQS model

Dynamics

In the basic feeding cycle model over one time step, mosquitoes either attempt to blood feed or attempt to lay eggs. The result of an attempt is either survival or death, and if the mosquito survives, success or failure. A success moves a mosquito to the other state, and if they fail, they must try again. Either way, the mosquito moves to a point in the set for the resource they seek:

The equations for sugar feeding are:

$$\begin{equation}\begin{array}{l} \left[ \begin{array}{c} B_t \\ Q_t \\ S_t \\ \end{array} \right] = \left[ \begin{array}{c} \Psi_{bq} \cdot p_q \hat \sigma_\Lambda \Lambda_{t-1} \\ 0 \\ \Psi_{sq} \cdot p_q \sigma_\Lambda \Lambda_{t-1} \\ \end{array} \right] + \left[ \begin{array}{ccc} \Psi_{bb} \cdot \mbox{diag}\left(\hat \sigma_b \hat \psi_b \right) & \Psi_{b q} \cdot \mbox{diag}\left(\hat \sigma_f \psi_q \right) & \Psi_{bs} \cdot \mbox{diag}\left(\psi_s \right) \\ \Psi_{qb} \cdot \mbox{diag}\left(\psi_b \right) & \Psi_{q q} \cdot \mbox{diag}\left( \hat \sigma_q \hat \psi_q \right)& \left(0\right) \\ \Psi_{sb} \cdot \mbox{diag}\left(\sigma_b \psi_b \right) & \Psi_{sq} \cdot \mbox{diag}\left(\left(\sigma_f \psi_q + \sigma_q \hat \psi_q \right)\right)& \Psi_{ss} \cdot \mbox{diag}\left(\hat \psi_s \right)\\ \end{array} \right] \left[ \begin{array}{c} p_b B_{t-1} \\ p_q Q_{t-1} \\ p_s S_{t-1} \end{array} \right] \end{array} \label{eq_BQS} \end{equation}$$