Mosquito Dispersal

Flight Bout

In a single flight bout, mosquito dispersal in a model is defined by point sets and dispersal kernels (i.e., $\Psi$). For mosquito populations, dispersal can be understood through these population dynamic models, where we are interested in describing movement to complete a phase of the feeding cycle, or through one complete feeding cycle.

A Behavioral State

Movement to accomplish a tasks could involve a sequence of search bouts, some of which may be unsuccessful. A functionally relevant measure of dispersal tracks movement: starting after laying eggs through failures until a surviving mosquito successfully blood feeds; or starting after blood feeding through failures until a mosquito successfully lays eggs.

Since there could be several failures, we modified the population dynamic models, creating a ``trap’’ algorithm to compute progress through a part of the feeding cycle. To do so, we modify the simulation by setting parameters to zero that determine the fraction of mosquitoes that would otherwise leave the state. We then initialize and follow a cohort, iterating until almost surviving mosquitoes are trapped in the end state (i.e., up to a predefined tolerance). We let $K_{b\leftarrow q}$ denote a $|b| \times |q|$ matrix describing net dispersal to blood feed once: it is the proportion of mosquitoes leaving $\left\{q\right\}$ after laying eggs that eventually blood feed successfully at each point in $\left\{b\right\}$. Similarly, we define $K_{q \leftarrow b}$ denote net dispersal to lay eggs starting after blood feeding.

The matrices generated by the trap variable algorithm describe movement through blood feeding and egg laying, even in models with sugar feeding. With sugar feeding, a mosquito that has laid eggs blood feed before laying again. A mosquito may fail to lay eggs and switch to sugar feeding, and then blood feed again before successfully laying eggs (see Figure 1). We can compute the matrices $K_{b\leftarrow q}$ and $K_{q \leftarrow b}$ accounting for the fact that a mosquito may sugar feed – possibly multiple times – before ending in the other state. Under the assumptions of this model, there may be some gonotrophic disassociation; a mosquito will always blood feed after sugar feeding, even if it was searching for aquatic habitat before the transition (see Figure). In such cases, $K_{b\leftarrow b}$ is the interval between blood meals with or without an egg batch, but because of the delay for parasite development, we must take even greater care in quantifying parasite dispersal by mosquitoes (see below).

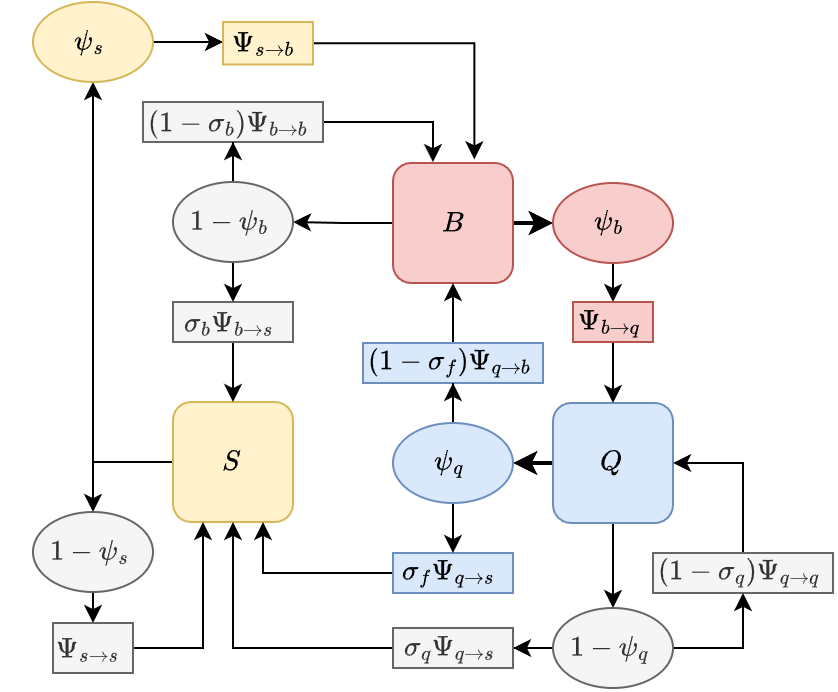
Figure 1: State transitions for the BQS model

A Feeding Cycle

The matrices $K_{bq}$ and $K_{qb}$ define a new, bipartite graph that describes movement among the point sets where mosquitoes lay eggs and where they blood feed (Fig~). In block form, movement through egg-laying and (possibly) sugar feeding can be represented in block form: % $$\begin{equation} K = \left[ \begin{array}{cc} 0 & K_{b \leftarrow q} \\ K_{q \leftarrow b} & 0 \end{array} \right] \label{KbqKqb} \end{equation}$$

After blood feeding and egg laying once – one complete feeding cycle – the bipartite graph disconnects into two complementary graphs on their respective point sets:

$$\begin{equation} K^2 = \left[\begin{array}{cc} K_{b \leftarrow b}& 0 \\ 0 & K_{q \leftarrow q} \end{array} \right] \label{KbbKqq} \end{equation}$$

The matrix $K_{b \leftarrow b} = K_{b \leftarrow q}\cdot K_{q \leftarrow b}$ describes movement from haunts to haunts, and $K_{q \leftarrow q}= K_{q \leftarrow b}\cdot K_{b \leftarrow q}$ describes movement from habitats to habitats.

Egg Laying

We developed algorithms to compute net dispersal of eggs away from a natal site. Net lifetime dispersal of eggs from natal aquatic habitats is summed over all gonotrophic cycles, $i$, until a mosquito has died. The expected number of eggs laid per emerging adult female at each site can be computed as:

$$\begin{equation} G = o \sum_{i=1}^\infty \left(K_{q\leftarrow q}\right)^i. \end{equation}$$

The quantity $G$ is mosquito lifetime egg dispersal kernel for a cohort. We also define net egg dispersal by the population at its steady state

$$\begin{equation} G \cdot \mbox{diag}\left(\bar Q \right), \end{equation}$$

where $\bar Q$ is the steady state density of adult female mosquitoes at $\left\{q\right\}$.

Pathogen Dispersal

We developed algorithms to compute potential dispersal of pathogens from the points where mosquitoes blood feeds. A basic formula for the dispersion of infective bites away from an infectious host must consider the delay for the extrinsic incubation period. Since chronological and reproductive age are not necessarily in sync, and since there might be gonotrophic disassociation, we can’t use $K_{b\rightarrow b}$. Instead, we simply run the simulation, summing up all potential transmission events, just as we would compute vectorial capacity.

Net dispersal of pathogens is computed by setting an initial cohort of mosquitoes that successfully took a blood meal, $B_0$, among haunts and iterating the model until all of the mosquitoes are dead. The number of infective bites given by the cohort is found by adding up all the bites after $\tau$ days, where $\tau$ is a parameter describing the EIP. Given $B_0$, we use the model to compute $B_t$ for a cohort of mosquitoes, and we define $V$ as

$$\begin{equation} V = \sum_{t=\tau}^\infty \mbox{diag} \left(\psi B_t \right). \end{equation}$$

While $V$ defines parasite dispersal by a cohort of mosquitoes, weighted evenly by point, we can also weight parasite dispersal by the steady state population density at each point, which we call potential pathogen dispersion, $P = V \cdot \mbox{diag}\left(\bar B \right)$, where $\bar B$ is the steady state density of adult female mosquitoes at $\left\{b\right\}$.

The matrix $P$ defines a quantity that differs slightly from the definition of vectorial capacity, in that it is not the expected number of bites arising from all the mosquitoes blood feeding on a single person. Instead, it is the expected number of infective bites arising from all the mosquitoes blood feeding at a single haunt on a single day, computed as if every available host was perfectly infectious. The quantity would be identical to if it were normalized by the number of hosts available ( modifying $B_0$), such that the quantity was an expected number arising from a single host.

Dispersal Distances

Any pair of matrices describing dispersal propensities among points in a set and the distances among points in that set can be normalized to define a probability distribution function. Since the number of destinations is finite, dispersal is described using probability mass functions (PMFs).