A Workhorse Model for Human Infection

suppressMessages(library(knitr))
suppressMessages(library(ramp.xds))
#suppressMessages(library(ramp.library))
library(deSolve)
library(ramp.library)
#devtools::load_all()

Warning: workhorse is in development.

In the following, we present a stage of infection (SoI) model for malaria infection that recognizes an important difference between the two major phases of an infection: the acute phase characterized by geometrically increasing parasite numbers; and the chronic phase characterized by fluctuating parasite densities. The model explicitly considers superinfection, which moves individuals from an infected state into a parallel set of states.

Uninfected individuals are either susceptible to infection $U$ or chemoprotected and not susceptible to infection.
Some recently treated, chemoprotected individuals remain infectious $G.$ The remainder are chemoprotected and not infectious, $P.$
There are four chronic infection stages: $I_{1},\ I_{2},\ I_{3}$ and $I_{4}$ .
There are five acute infection stages: four ( $A_{1},\ A_{2},\ A_{3},\ A_{4}$ ) that correspond to an acute-phase infection concurrently infected with parasites in the chronic phase; and one ( $A_{0}$ ) that corresponds to carrying an acute phase infection but being otherwise uninfected.
All acutely infected individuals transition into $I_1$

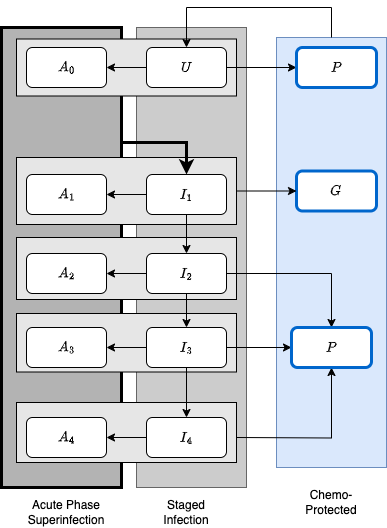
Variables

The variables are thus:

$U$
Chemoprotected states are $P$ and $G$
Acute stages of infection: $A_{0},\ A_{1},\ A_{2},\ A_{3},\ A_{4}$
Chronic stages of infection: $I_{1},\ I_{2},\ I_{3},\ I_{4}$

Parameters

These are:

$r$ - the rate of recovery from infection
$\sigma$ - treatment rate
$h_{\tau}$ - rate at which immunity is acquired
$\zeta_{U}$ - rate at which chemoprophylaxis is administered to uninfected individuals
$\zeta_{A}$ - rate at which chemoprophylaxis is administered to individuals in acute phase of infection
$\phi$ - rate at which individuals in acute phase move into chronic stage of infection
$\zeta_{i}, i= 1,2,3,4$ - rate at which individuals in chronic stages of infection obtain chemoprophylaxis
$p(w)$ - the peak of infection
$\xi_{i},i=1,2,3,4$ - rate at which individuals move through the different chronic stages of infection
$\delta_{I}$ - rate of loss of immunity

Active acute-phase infections become apparent after $\tau$ days, and:

Uninfected

$\begin{array}{rl} \frac{dU}{da} &= r \sum_i I_i + \sigma (P + G) - (h_\tau + \zeta_U) U \\ \frac{dA_0}{da} &= r \sum_i A_i + h_\tau U - (\phi + \zeta_A + \zeta_U) A_0 \end{array}$ Chemoprotected

We are assuming that treatment as a result of an acute infection could leave a person infectious:

$\begin{array}{rl} \frac{dP}{da} &= \zeta_U (U + A_0) + \sum_{i\geq 2} \zeta_i I_i - \sigma P \\ \frac{dG}{da} &= \zeta_1 I_1 + \zeta_A \sum_i A_i - \sigma G \\ \end{array}$

Infected

Where $\phi$ is on the order of $1/10 d$ and

At peak:

$\begin{array}{rl} \frac{dI_1}{da} & = p(w) \phi \sum_i A_i - (h_\tau + r + \xi_1 + \zeta_1) I_1 \\ \frac{dI_2}{da} & = (1-p(w)) \phi \sum_i A_i + \xi_1 I_1 - (h_\tau + r + \xi_2+ \zeta_2) I_2 \\ \frac{dI_3}{da} & = \xi_2 I_2 - (h_\tau + r + \xi_3 + \zeta_3) I_3 \\ \frac{dI_4}{da} & = \xi_3 I_3 - (h_\tau + r + \zeta_4) I_4 \\ \end{array}$

Past peak, for $n \in 2,3,4$ :

$\begin{array}{rl} \frac{dA_1}{da} & = h_\tau I_1 - \phi A_1 - (\zeta_A + r + \zeta_1) A_1 \\ \frac{d A_n}{da} &= h_\tau I_n - \phi A_n - (\zeta_A + \zeta_n) I_n\\ \end{array}$ Immune Tracking

$\begin{array}{rl} \frac{d w_0}{da} &= h_\tau \\ \frac{d w_i}{da} &= h_\tau - \delta_I w_i \\ \end{array}$

#devtools::load_all()

wh <- xds_setup(dlay = 'dde', 
                Xname = "workhorse", 
                HPop=1000,
                Lname = "trivial", 
                Lopts = list(
                  Lambda = 3000, 
                  season = function(t){1+sin(2*pi*t/365)}
                  )
                )

wh <- xde_solve(wh, Tmax = 5*365, dt=10)

wh1 = wh 
wh1$Xpar[[1]]$zeta_1 = 0.02
wh1 <- xde_solve(wh1, Tmax = 5*365, dt=10)

xds_plot_X(wh)
xds_plot_X(wh1, llty=2, add=FALSE)

time = wh$outputs$time
with(wh$outputs$orbits$XH[[1]],{
  A = A0+A1+A2+A3+A4
  I = I1+I2+I3+I4
  plot(time, U + P + G, type = "l", ylim = range(0, H), col = "darkblue") 
  lines(time, A+I, col = "darkred") 
  lines(time, A, col = "purple") 
  lines(time, I-I1, col = "orange") 
  lines(time, P+G, col = "darkgreen") 
})

with(wh1$outputs$orbits$XH[[1]],{
  A = A0+A1+A2+A3+A4
  I = I1+I2+I3+I4
  lines(time, U + P + G, col = "darkblue", lty=2) 
  lines(time, A+I, col = "darkred", lty=2) 
  lines(time, A, col = "purple", lty=2) 
  lines(time, I-I1, col = "orange", lty=2) 
  lines(time, P+G, col = "darkgreen", lty=2) 
})

July 14, 2025

Variables

Parameters