The adult mosquito model RMG

library(knitr)
library(ramp.xds)
library(deSolve) 
library(ramp.library)

Most of the models developed to model malaria parasite infections in mosquitoes look at the infection states: uninfected; infected; or infected and infectious. A few models have been developed that track also track parity. A different class of models tracks the behavioral / physiological state of mosquitoes, so we call them behavioral state models. A model with both infection states and behavioral states was first published by Le Menach, et al. (2005)¹.

The Model

This is a patch-based model with $p$ patches, and we assume that all the parameters, variables, and terms are of length $p$ except for $\Omega_b$ and $\Omega_q$ , which are $p \times p$ matrices.

Variables

$U_b$ - uninfected, blood feeding mosquitoes
$U_q$ - uninfected, egg laying mosquitoes
$Y_b$ - infected but not infective, blood feeding mosquitoes
$Y_q$ - infected but not infective, egg laying mosquitoes
$Z_b$ - infective, blood feeding mosquitoes
$Z_q$ - infective, egg laying mosquitoes

Terms

Two terms are passed from another component of the model.

$\Lambda$ - the emergence rate of adult mosquitoes from aquatic habitats in each patch
$\kappa$ - the net infectiousness of humans, the probability a mosquito becomes infected after blood feeding on a human

Parameters

Bionomics - Each one of the following parameters can take on a unique value in each patch.

$f$ - the blood feeding rate
$q$ - the human blood feeding fraction
$\nu$ - the egg laying rate
$g$ - the mosquito death rate, per mosquito
$\varphi$ - the rate that infected mosquitoes become infective, the inverse of the EIP
$\sigma_b$ - the patch emigration rate for blood-feeding mosquitoes
$\sigma_q$ - the patch emigration rate for egg-laying mosquitoes
$\mu$ - the emigration loss rate: excess mortality associated with migration

Dipsersal Matrices - Each one of the following parameters can take on a unique value in each patch.

${\cal K}_b$ - the dispersal matrix for blood-feeding mosquitoes, which has the form: ${\cal K} = \left[ \begin{array}{ccccl} 0 & k_{1,2} & k_{1,3} & \ldots & k_{1,p} \\ k_{2,1} & 0 & k_{2,3} & \ldots & k_{2,p} \\ k_{3,1} & k_{3,2} & 0 & \ldots & k_{3,p} \\ \vdots& \vdots &\vdots & \ddots & k_{p-1, p} \\ k_{p,1} & k_{p,2} & k_{p,3} & \ldots & 0 \\ \end{array} \right].$ The diagonal elements are all $0$ , and other elements, $k_{i,j} \in {\cal K}$, are the fraction of blood feeding mosquitoes leaving patch $j$ that end up in patch $i$ ; the notation should be read as $i \leftarrow j$ , or to $i$ from $j$ . Notably, the form of $\cal K$ is constrained such that $\sum_i k_{i,j} = 1.$
${\cal K}_q$ - the dispersal matrix for egg-laying mosquitoes, which has the same form as ${\cal K}_b$

The Demographic Matrices

$\Omega_b$ - the demographic matrix for blood feeding mosquitoes; letting $I$ denote the identity matrix, $\Omega_b = \mbox{diag}\left(g\right) - \mbox{diag}\left(\sigma_b\right) \left(\mbox{diag}\left(1-\mu\right) - \cal K_b \right)$
$\Omega_q$ - the demographic matrix for egg laying mosquitoes; which has the same form as $\Omega_b$ .

Dynamics

The following equations track adult mosquito behavioral and infection dynamics. A key assumption is that a fraction $q\kappa$ of blood feeding, uninfected mosquitoes become infected, thus transition from $U_b$ to $Y_g.$

$\begin{array}{rl} \dfrac{dU_b}{dt} &= \Lambda + \nu U_g - f U_b - \Omega_b \cdot U_b \\ \dfrac{dU_g}{dt} &= f (1- q \kappa) U_b - \nu U_g - \Omega_g \cdot U_g \\ \dfrac{dY_b}{dt} &= \nu Y_g + \phi Y_g - (f+\varphi) Y_g - \Omega_b \cdot Y_b \\ \dfrac{dY_g}{dt} &= f q \kappa U_b + f Y_b - (\nu + \varphi) Y_g - \Omega_g \cdot Y_g \\ \dfrac{dZ_b}{dt} &= \varphi Y_b + \nu Z_g - f Z - \Omega_b \cdot Z_b \\ \dfrac{dZ_g}{dt} &= \varphi Y_g + f Z - \nu Z - \Omega_q \cdot Z_q \end{array}$

Implementation

The xds_setup() utilities allow the user to pass a single version of the dispersal matrix $\cal K.$ During xds_setup(), Omega_b and Omega_q are identical.

HPop = rep(1000, 3)
residence = c(1:3) 
model <- xds_setup(MYZname="RMG", Lname="trivial", Xname = "trivial",  residence=residence, HPop =HPop, nPatches=3)

model <- xds_solve(model, dt=5)

par(mfrow = c(2,1))
xds_plot_M(model)
xds_plot_YZ(model, add_axes = F)
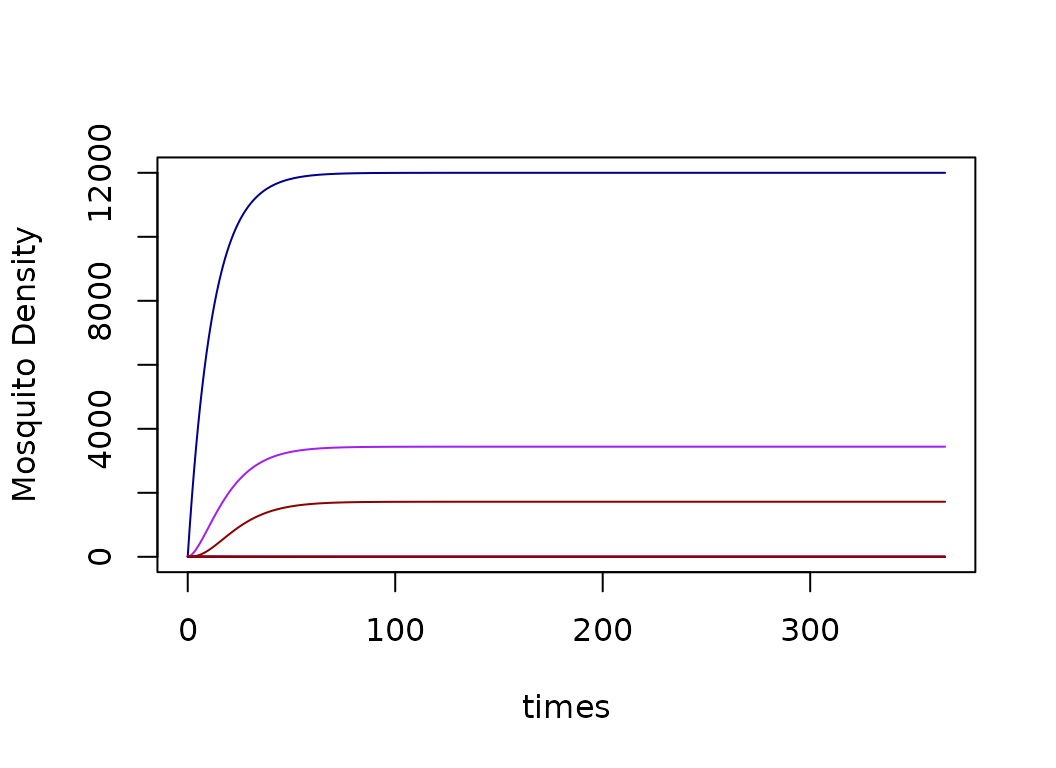
xds_plot_YZ_fracs(model)

xds_plot_YZ_fracs(model)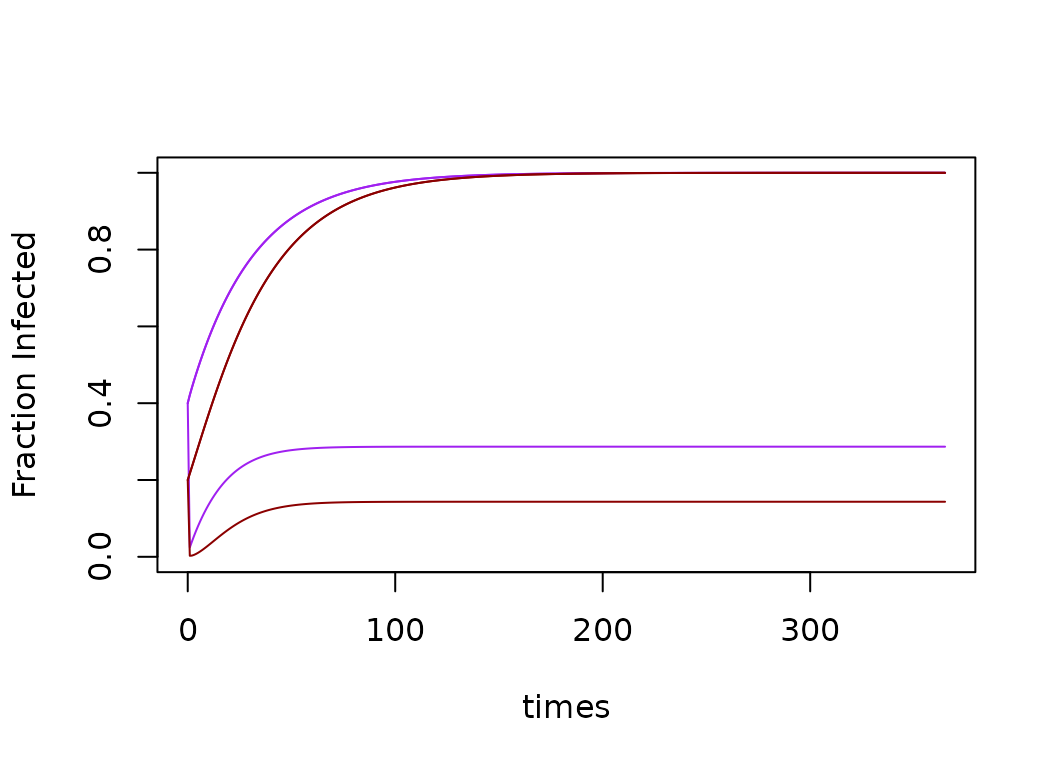

Menach AL, et al. The unexpected importance of mosquito oviposition behaviour for malaria: non-productive larval habitats can be sources for malaria transmission. Malar J 4, 23 (2005). https://doi.org/10.1186/1475-2875-4-23 ↩︎