Compartmental Models

October 16, 2024

library(knitr)
library(ramp.xds)
library(ramp.library)
library(deSolve)
library(ramp.library)

In this vignette, we describe four basic compartmental models for mosquito-borne pathogens commonly used for humans in ramp.library. The models are named by their states: susceptible (S) - exposed (E) infected (I) - recovered and immune (R), and vaccinated (V). According to their setup, not all models include all of the states. There are four compartmental models: SIR, SIRS, SEIR, and SEIRV. The other models including SIS, SEI and SIP and SEIS are described in the ramp.xds.

Model Variables

  • SS is the density of susceptible humans

  • EE is the density of exposed humans

  • II is the density of infected humans

  • RR is the density of recovered and immune humans

  • VV is the density of vaccinated humans

  • HH is the density of humans

Parameters

  • rr is the rate infections clear

  • bb is the fraction of bites by infective mosquitoes that transmit parasites and cause an infection.

  • cc is the fraction of bites on an infectious human that would infect a mosquito.

  • ε\varepsilon proportion of recovered individuals progressing into vaccinated class

  • α\alpha is a proportion of vaccinated humans

  • τ\tau is the rate at which exposed humans become infectious (incubation rate)

  • γ\gamma rate at which recovered human loss their immunity

  • δ\delta proportion of recovered humans progressing to vaccinated class

Dynamics

The models defined herein is defined in two parts. To model exposure and infection (i.e. the conversion of EIR into FoI (h)), The equations are formulated around hh. Under the default model, we get the relationship h=bEh=bE, where E is the daily EIR:

The dynamics of Susceptible-Infected- Recovered (SIR) are given by:

dSdt=B(H)−hS−μSdIdt=hS−(r+μ)IdRdt=rI−μR \begin{eqnarray*} \frac{dS}{dt} &=&B(H) - h S - \mu S\\ \frac{dI}{dt} &=& h S- (r +\mu) I\\ \frac{dR}{dt} &=& r I- \mu R \end{eqnarray*} Without demography i.e $ B(H) = = 0$, SIR model has steady states as S‾=0,I‾=0,R‾=H \bar{S} = 0, \quad \bar{I} =0, \quad \bar{R} = H.

The dynamics of Susceptible-Infected- Recovered -Suscepitible (SIRS) are given by:

dSdt=B(H)−hS+γR−μSdIdt=hS−(r+μ)IdRdt=rI−(μ+γ)R \begin{eqnarray*} \frac{dS}{dt} &=& B(H) - h S + \gamma R - \mu S\\ \frac{dI}{dt} &=& h S- (r +\mu) I\\ \frac{dR}{dt} &=& r I- (\mu+ \gamma) R \end{eqnarray*} Without demography, the SIRS model has the following steady states as

I‾=hHγrγ+h(γ+r)R‾=hrHrγ+h(γ+r)S‾=H−I‾−R‾ \begin{eqnarray*} \bar{I} &=& \frac{h H\gamma}{r\gamma + h(\gamma+r) }\\ \bar{R} &=& \frac{h r H}{r\gamma + h(\gamma+r) }\\ \bar{S} &=& H- \bar{I}-\bar{R} \end{eqnarray*}

The dynamics of Susceptible -Exposed -Infected- Recovered (SEIR) are given by:

dSdt=B(H)−hS−μSdEdt=hS−τE−μEdIdt=τE−(r+μ)IdRdt=rI−μR \begin{eqnarray*} \frac{dS}{dt} &=& B(H) - h S - \mu S\\ \frac{dE}{dt} &=& hS - \tau E- \mu E\\ \frac{dI}{dt} &=& \tau E- (r +\mu) I\\ \frac{dR}{dt} &=& r I- \mu R \end{eqnarray*} Without demography, the SEIR model has the steady states given as S‾=0,E‾=0,I‾=0,R‾=H \bar{S} = 0, \quad \bar{E} = 0,\quad \bar{I} = 0,\quad \bar{R} = H

The dynamics of Susceptible-Infected- Recovered -Suscepitible- Vaccinated (SEIRV) are based on the are given by:

dSdt=(1−α)B(H)−hS+γR−μSdEdt=hS−(τ+μ)EdIdt=τE−(r+μ)IdRdt=(1−ε)rI−(γ+μ)RdVdt=αB(H)+εrI−μV\begin{eqnarray} \frac{dS}{dt} &=&(1-\alpha)B(H) - h S + \gamma R - \mu S\\ \frac{dE}{dt} &=& h S - (\tau + \mu)E\\ \frac{dI}{dt} &= &\tau E - (r +\mu) I\\ \frac{dR}{dt} &=& (1-\varepsilon) r I- (\gamma+\mu) R\\ \frac{dV}{dt} &=& \alpha B(H)+ \varepsilon r I -\mu V \end{eqnarray} Without demography, the SEIRV has the following steady states: S‾=0,E‾=0,I‾=0,R‾=0,V‾=H \bar{S} = 0, \quad \bar{E} = 0,\quad \bar{I} = 0,\quad \bar{R} = 0,\quad \bar{V}= H

Terms

Net Infectiousness

True prevalence is:

x=XH.x = \frac{X}{H}.

In our implementation, net infectiousness (NI) is linearly proportional to prevalence:

ni=cx.ni = c x.

Human Transmitting Capacity

After exposure, a human would remain infected for 1/r1/r days, transmitting with probability cc so:

HTC=c/rHTC= c/r

Example ramp.xds Setup

We run each of the models using a default setup with 1- stratum to equilibrium and compare our results with the analytic steady states given above

test_SIR<- xds_setup(MYZname="macdonald", Xname="SIR")
xds_solve(test_SIR, 365*5) -> test_SIR
foi_eq = test_SIR$Xpar[[1]]$b*tail(test_SIR$outputs$terms$EIR,1)
unlist(list_Xvars(test_SIR$outputs$last_y, test_SIR, 1)) -> inf 
xde_steady_state_X(foi_eq, 1000, test_SIR$Xpar[[1]]) -> ss
xds_plot_X(test_SIR)

test_SIRS<- xds_setup(MYZname="macdonald", Xname="SIRS")
xds_solve(test_SIRS, 365*3) -> test_SIRS
foi_eq = test_SIRS$Xpar[[1]]$b*tail(test_SIRS$outputs$terms$EIR,1)
unlist(list_Xvars(test_SIRS$outputs$last_y, test_SIRS, 1)) -> inf_SIRS
xde_steady_state_X(foi_eq, 1000, test_SIRS$Xpar[[1]]) -> ss_SIRS
xds_plot_X(test_SIRS)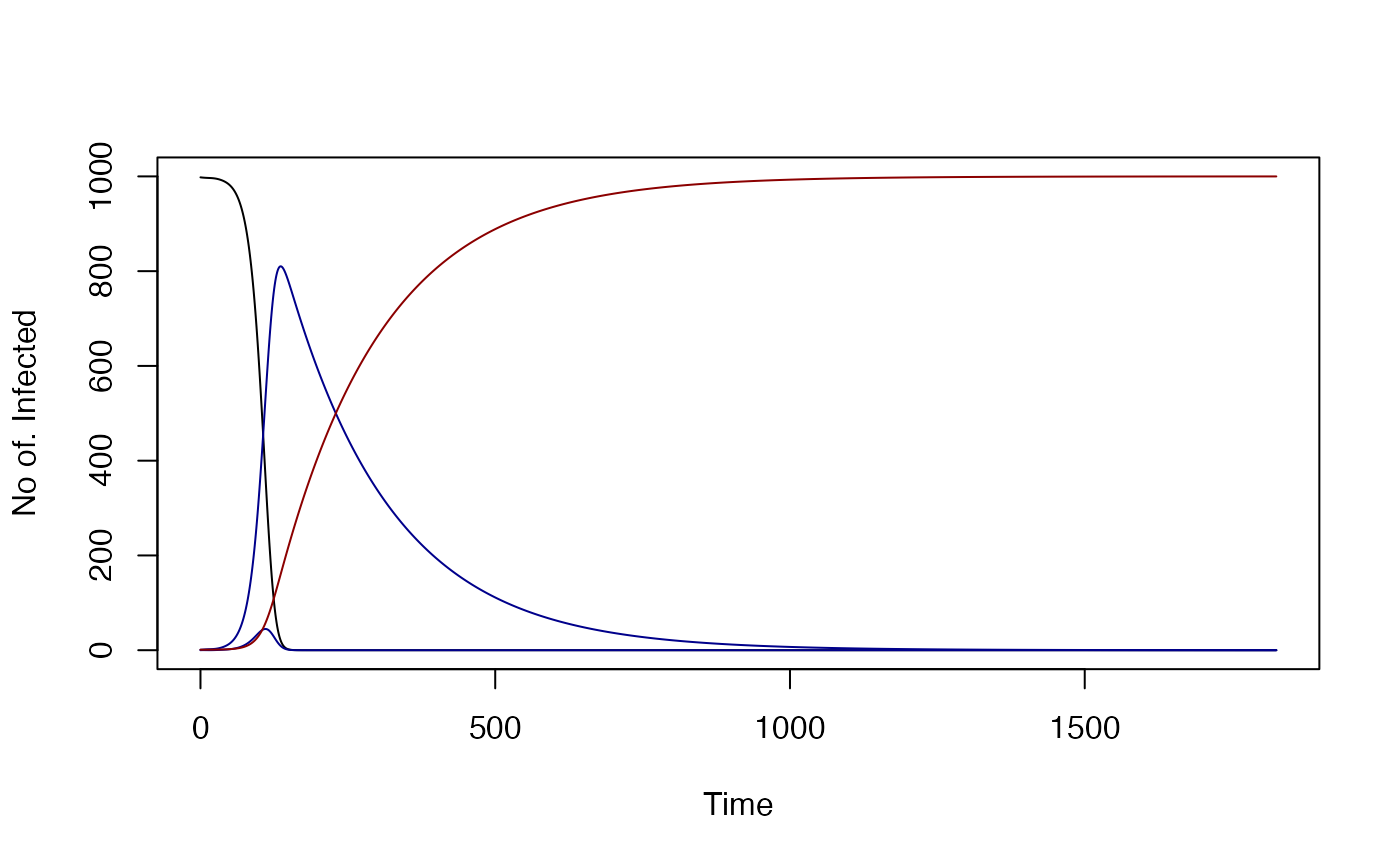

test_SEIR<- xds_setup(MYZname="macdonald", Xname="SEIR")
xds_solve(test_SEIR, 365*5) -> test_SEIR
foi_eq = test_SEIR$Xpar[[1]]$b*tail(test_SEIR$outputs$terms$EIR,1)
unlist(list_Xvars(test_SEIR$outputs$last_y, test_SEIR, 1)) -> inf_SEIR
xde_steady_state_X(foi_eq, 1000, test_SEIR$Xpar[[1]]) -> ss_SEIR
xds_plot_X(test_SEIR)

test_SEIRV<- xds_setup(MYZname="macdonald", Xname="SEIRV")
xds_solve(test_SEIRV, 365*5) -> test_SEIRV
foi_eq = test_SEIRV$Xpar[[1]]$b*tail(test_SEIRV$outputs$terms$EIR,1)
unlist(list_Xvars(test_SEIRV$outputs$last_y, test_SEIRV, 1)) -> inf_SEIRV
xde_steady_state_X(foi_eq, 1000, test_SEIRV$Xpar[[1]]) -> ss_SEIRV
xds_plot_X(test_SEIRV)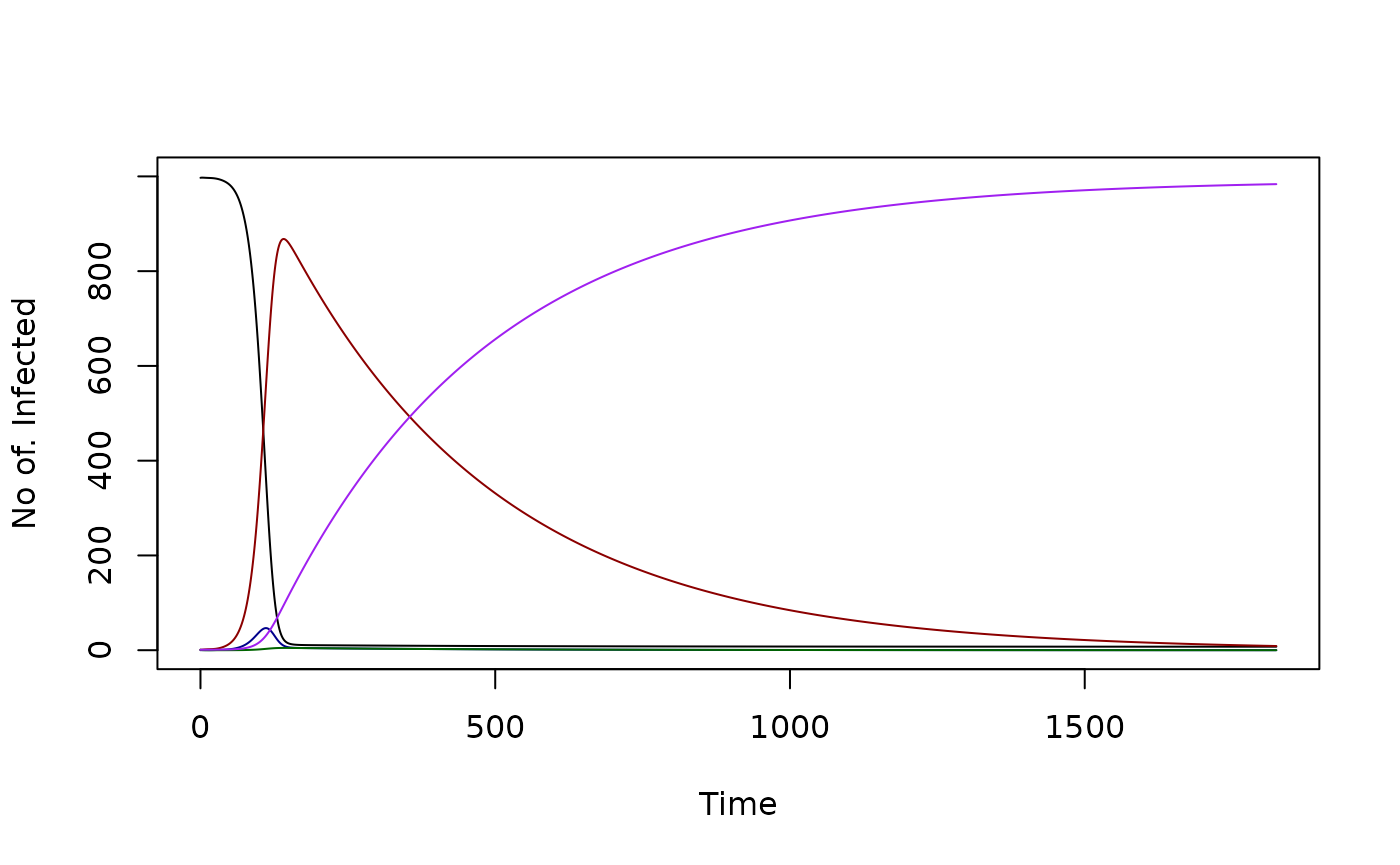

References

  1. Ross R. Report on the Prevention of Malaria in Mauritius. London: Waterlow; 1908.
  2. Ross R. The Prevention of Malaria. 2nd ed. London: John Murray; 1911.
  3. Smith DL, Battle KE, Hay SI, Barker CM, Scott TW, McKenzie FE. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012;8: e1002588. doi:10.1371/journal.ppat.1002588