SIP: an XH Module

Susceptible, Infected, and post-treatment Protection

The SIP (Susceptible-Infected-Protected) human model model implements a basic model for human infection with malaria that includes an extra state for post-treatment chemoprotection, a short period when a person is protected from being infected.

It is a reasonable first complication of the ramp.xds::SIS human model. This requires new parameters: $\rho$, the probability a new infection is treated; $\sigma$ is treatment of malaria infections; $\xi$ is background treatment; and $\eta$ the duration of chemoprophylaxis following treatment. $X$ remains a column vector giving the infectiuos density of infectious individuals in each strata, and $P$ the number of treated and protected individuals.

Differential Equations

The equations are formulated around the FoI, $h$. Under the default model, we get the relationship $h = b E$, where $E$ is the daily EIR:

$$\frac{dH}{dt} = F_B(t, H) - D \cdot H$$

$$\frac{dI}{dt} = h (1-\rho) (H-I-P) - (r+\xi+\sigma)I + D \cdot I$$

$$\frac{dP}{dt} = h \rho (H-I-P) + \xi(H-P) + \sigma I - \eta P + D \cdot P$$ In the model $$X = c I/ H.$$

Equilibrium solutions

We can compute the steady states as a function of the FoI, $h$:

$$\bar I = H \frac{h \eta (1-\rho)}{(h+r+\xi+\sigma)(\eta+\xi) +h((r-\eta)\rho+\sigma)}$$ and

$$\bar P = H\frac{\xi(h+r+\xi+\sigma) + h(r\rho+\sigma)}{(h+r+\xi+\sigma)(\eta+\xi) +h((r-\eta)\rho+\sigma)}$$ and $$\bar S = H - \bar I - \bar P$$

Example

library(ramp.xds)
library(ramp.library)
library(deSolve)
library(data.table)
library(ggplot2)

Here we run a simple example with 3 population strata at equilibrium. We use ramp.xds::make_parameters_X_SIP_xde to set up parameters. Please note that this only runs the human population component and that most users should read our fully worked example to run a full simulation.

We use the null (constant) model of human demography ($H$ constant for all time).

The Long Way

nStrata <- 3
H <- c(100, 500, 250)
nPatches <- 3
residence <- 1:3 
params <- make_xds_object_template("ode", "human", nPatches, 1, residence) 

b <- 0.5
c <- 0.15
r <- 1/200
eta <- c(1/30, 1/40, 1/35)
rho <- c(0.05, 0.1, 0.15)
xi <- rep(0, 3)
sigma <-rep(0.5,3)
Xo = list(b=b,c=c,r=r,eta=eta,rho=rho,sigma=sigma,xi=xi)
params = setup_XH_obj("SIP", params, 1, Xo) 

eir <- c(1,2,3)/365
steady_state_X(eir*b, H, params) -> ss
params = setup_XH_inits(params, H, 1, ss)

Xo <- c(Xo, ss) 

MYo = list(
  Z = eir*H, f=1, q=1
)

params = setup_MY_obj("trivial", params, 1, MYo)
params = setup_MY_inits(params, 1)
params = setup_L_obj("trivial", params, 1)
params = setup_L_inits(params, 1)

params = make_indices(params)

steady_state_X(eir*b, H, params, 1)
#> $H
#> [1] 100 500 250
#> 
#> $I
#> [1] 0.2470051 2.1925016 1.5043227
#> 
#> $P
#> [1]  3.90203 48.77098 31.01781

y0 <- as.vector(unlist(get_inits(params)))

out <- deSolve::ode(y = y0, times = c(0, 730), xde_derivatives, parms= params, method = 'lsoda') 
get_XH_vars(out[2,-1], params, 1)
#> $S
#>         1         2         3 
#>  95.85096 449.03652 217.47787 
#> 
#> $I
#>         4         5         6 
#> 0.2470051 2.1925016 1.5043227 
#> 
#> $P
#>        7        8        9 
#>  3.90203 48.77098 31.01781 
#> 
#> $H
#>   1   2   3 
#> 100 500 250

colnames(out)[params$XH_obj[[1]]$ix$H_ix+1] <- paste0('H_', 1:params$nStrata)
colnames(out)[params$XH_obj[[1]]$ix$I_ix+1] <- paste0('I_', 1:params$nStrata)
colnames(out)[params$XH_obj[[1]]$ix$P_ix+1] <- paste0('P_', 1:params$nStrata)

out <- as.data.table(out)
out <- melt(out, id.vars = 'time')
out[, c("Component", "Strata") := tstrsplit(variable, '_', fixed = TRUE)]
out[, variable := NULL]

ggplot(data = out, mapping = aes(x = time, y = value, color = Strata)) +
  geom_line() +
  facet_wrap(. ~ Component, scales = 'free') +
  theme_bw()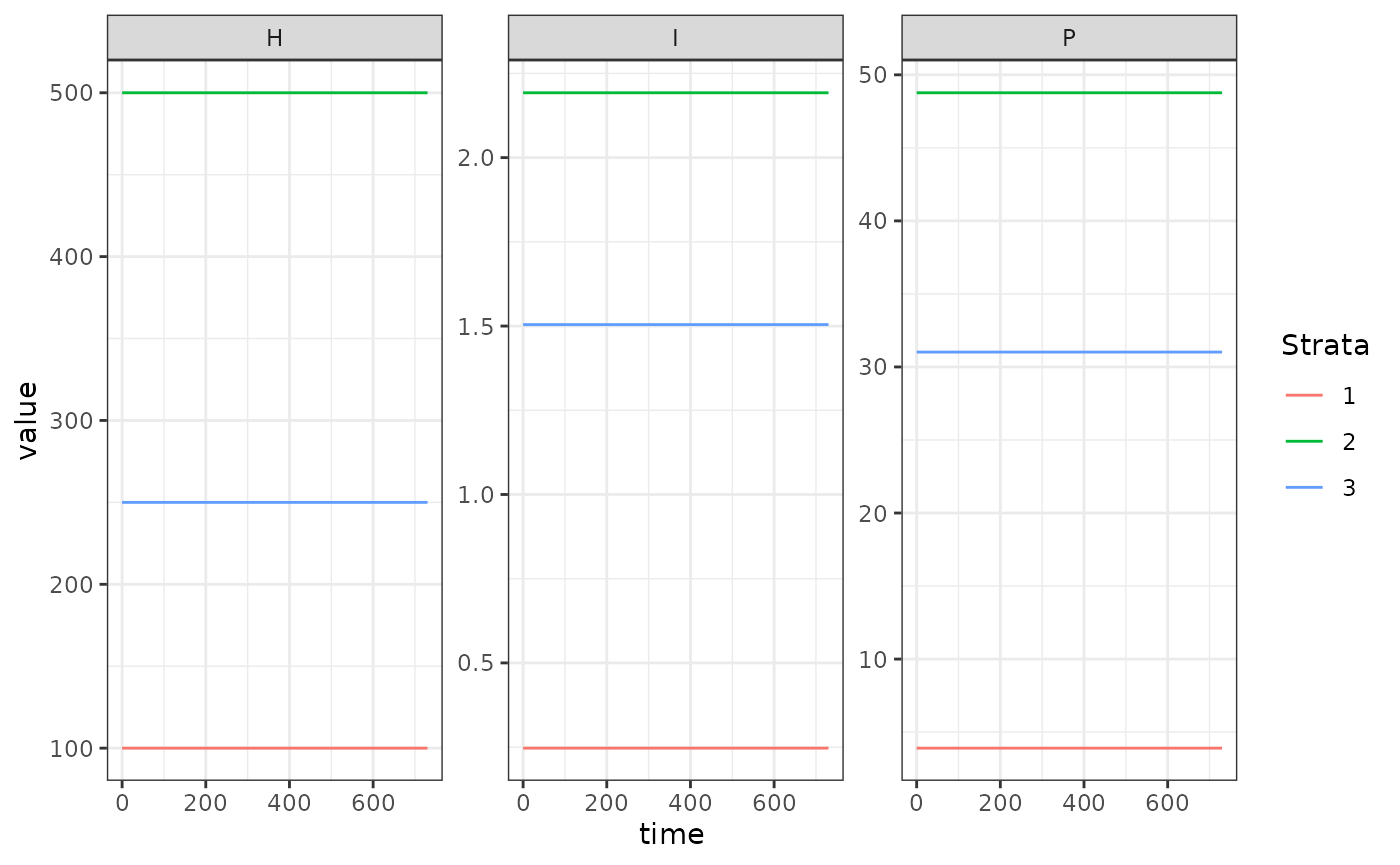

Using Setup

xds_setup_human(Xname="SIP", nPatches=3, residence = 1:3, HPop=H, XHoptions= Xo, MYoptions = MYo) -> test_SIP_xde

steady_state_X(b*eir, H, test_SIP_xde, 1) -> out1
out1 <- unlist(out1)

xds_solve(test_SIP_xde, 365, 365)$outputs$last_y -> out2
approx_equal(out2,out1) 
#>         1    2    3    4    5    6    7    8    9
#> [2,] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE