An important role for mathematical models is to understand dynamical responses to malaria control, or response timelines: how would the system respond to major perturbations? This is highly relevant for the evaluation of vector control, which is often implemented as mass bed net distributions or mass indoor residual spraying (IRS) events.
Perturbations
In his 1982 book, The Biomathematics of Malaria, Bailey introduces dynamical systems describing malaria up to that point. The chapters focus on 1) threshold criteria and epidemics in malaria-naive populations; and 2) understanding endemic malaria. Here, we consider response timelines, the dynamical responses to perturbations.
In vector control, a basic notion is the concept of an effect size, or a proportional change in a quantity of interest. For an effect size to be a meaningful quantity, it must be defined around the way vector control actually happens. In this context, and being someone generic for now, vector control coverage undergoes a rapid increase followed by a long decay. The effects of vector control change dynamically as coverage changes. Here, we define a response timeline as a set of curves describing the effects of malaria vector control over time.
Vector control is often implemented through mass distribution events: mass bed net distributions; or mass indoor residual spraying (IRS). In a mechanistic model, the direct effect of the distribution is to modify blood feeding and mosquito survival. In the case of bed nets, the nets also modify exposure when they are used. Causation here involves complex cascading chains. For bednets: access, use, mosquito contact, and effect. For IRS, coverage, killing potential, mosquito contact and effect.
SimBA was developed to handle these phenomena in several ways. Peer reviewed mechanistic models can trace the effects of vector control on bionomic parameters, effects on mosquito aquatic ecology. There are also built in functions to model forcing by the EIR directly. An important role for mathematical models is to help develop rational expectations about the changes in the prevalence of infection in humans.
PR Response Timelines
For planning purposes, the Global Malaria Eradication Programme (GMEP) set 200 days as the expected decay in prevalence following the complete interruption of transmission. What should we expect to see in the wake of a mass bed net distribution program or in the wake of IRS?
SimBA was developed with functions to compose and decompose time
series. A forcing function can be composed that is the product of a
mean, a seasonal pattern, a trend, and some shocks. To model the shocks,
SimBA developed sharkbite functions to mimic vector control
coverage and effects over time. A sharkbite is the product
of two sigmoidal functions with a start date, a duration, shape
parameters that set the slope, and a maximum value.
This function creates an effect that starts on day 500, ramps up rapidly to a maximum of 50%, and then then declines, reaching 50% of its maximum after 365 days.
tt <- seq(0, 5*365, by=5)
p1 <- makepar_F_sharkbite(500, 365, dk = 1/100, mx=0.8)
F1 <- make_function(p1)
plot(tt, F1(tt), type = "l", xlab = "Time", ylab = "Effect Size", main = "Response Timeline", ylim = c(0,1))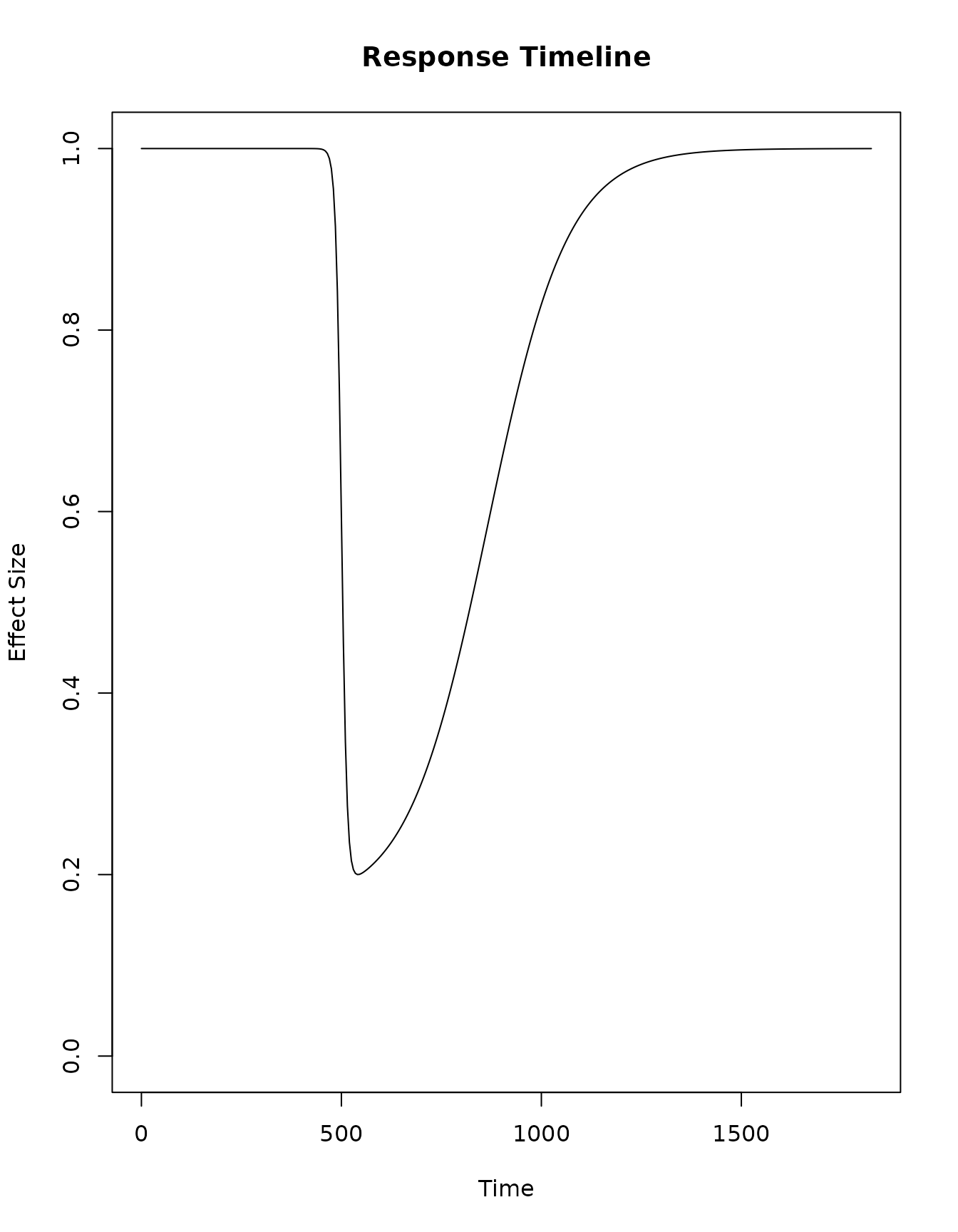 We can use it to modify exposure in a model, and see how malaria
prevalence responds.
We can use it to modify exposure in a model, and see how malaria
prevalence responds.
par(mfrow = c(2,1))
sis_si_eir <- xds_setup_eir(Xname = "SIS", shock_par = p1, eir=3/365)
sis_si_eir <- burnin(sis_si_eir)
sis_si_eir <- xds_solve(sis_si_eir, 5*365, 5)
xds_plot_EIR(sis_si_eir) -> eir
xds_plot_PR(sis_si_eir) -> pr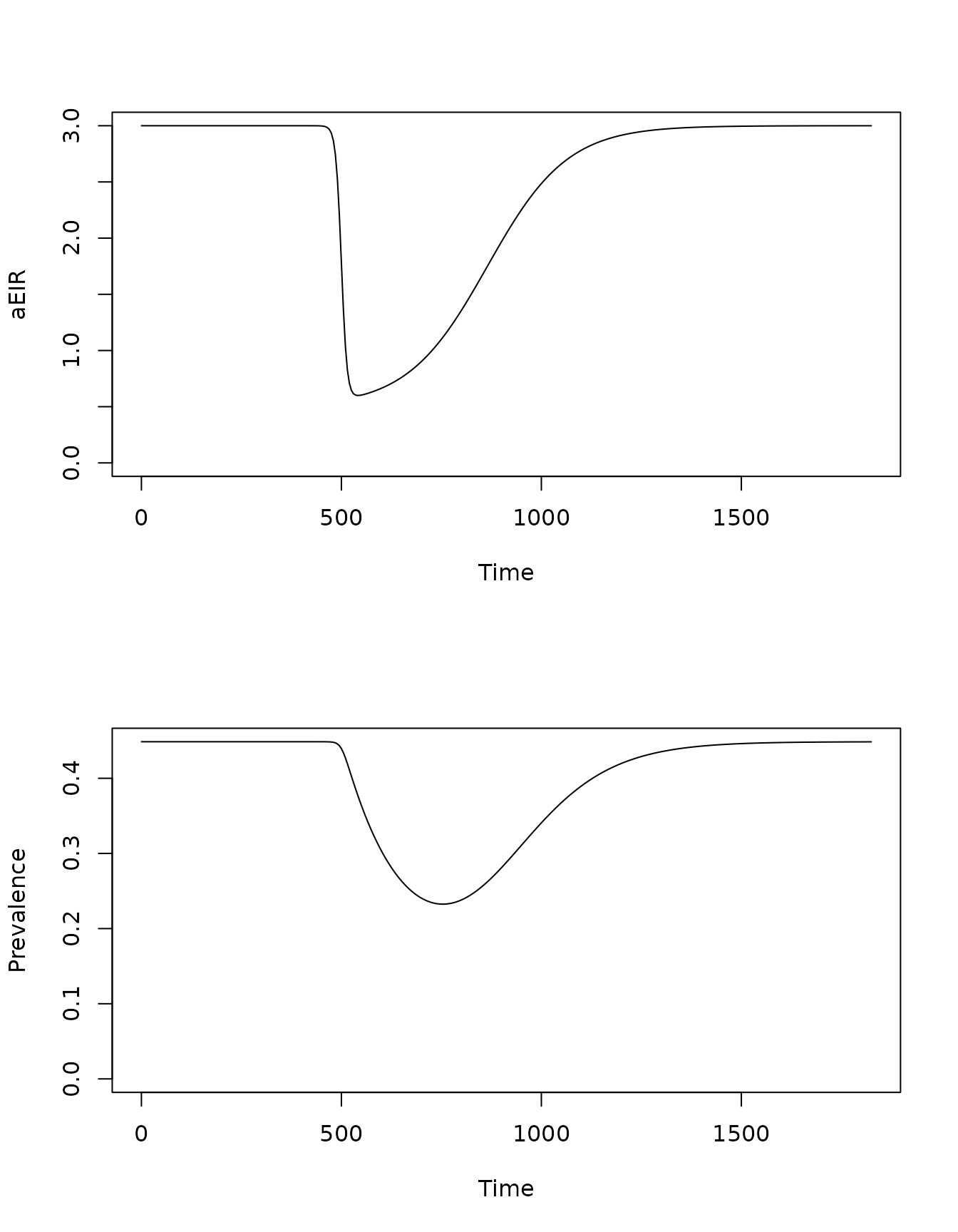
What we observe is a decline in PfPR starting shortly after the perturbation happens, and then a recovery to the steady state.
What if malaria is seasonal?
par(mfrow = c(2,1))
seas0 = makepar_F_sin(bottom = 0.3, pw=2)
sis_si_eir_1 <- xds_setup_eir(Xname = "SIS", season_par = seas0, eir=3/365)
sis_si_eir_2 <- xds_setup_eir(Xname = "SIS", season_par = seas0, shock_par = p1, eir=3/365)
sis_si_eir_1 <- burnin(sis_si_eir_1)
sis_si_eir_2 <- burnin(sis_si_eir_2)
sis_si_eir_1 <- xds_solve(sis_si_eir_1, 5*365, 5)
sis_si_eir_2 <- xds_solve(sis_si_eir_2, 5*365, 5)
xds_plot_EIR(sis_si_eir_2) -> eir2
get_EIR(sis_si_eir_1) -> eir1
xds_plot_PR(sis_si_eir_2) -> pr2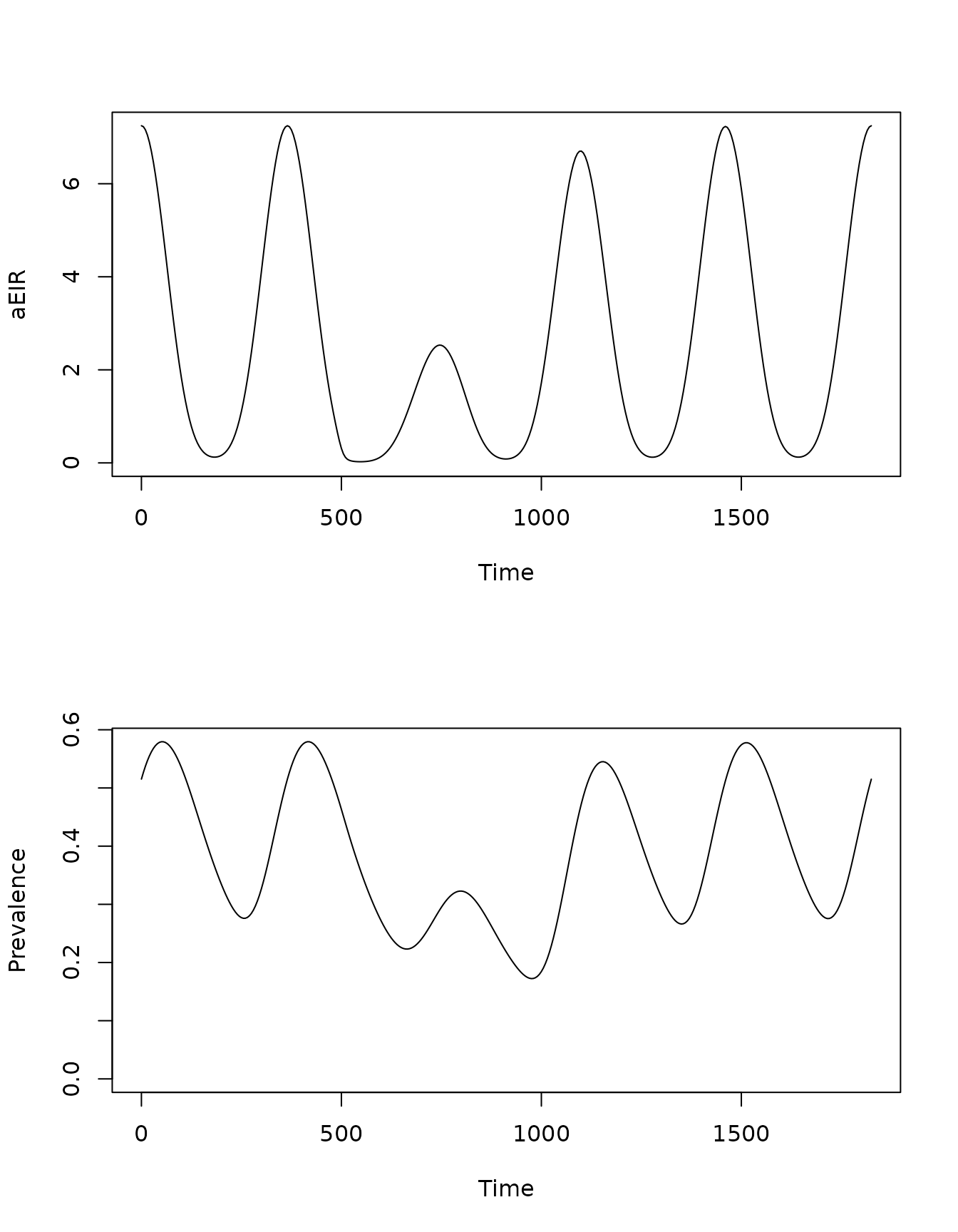
get_PR(sis_si_eir_1) -> pr1 Now, the effect is modulated by the seasonal pattern. Here we show the effects on EIR and PR as ratios and differences.
tt=seq(0, 5*365, by = 5)
par(mfcol = c(2,2), mar = c(3,5,2,1))
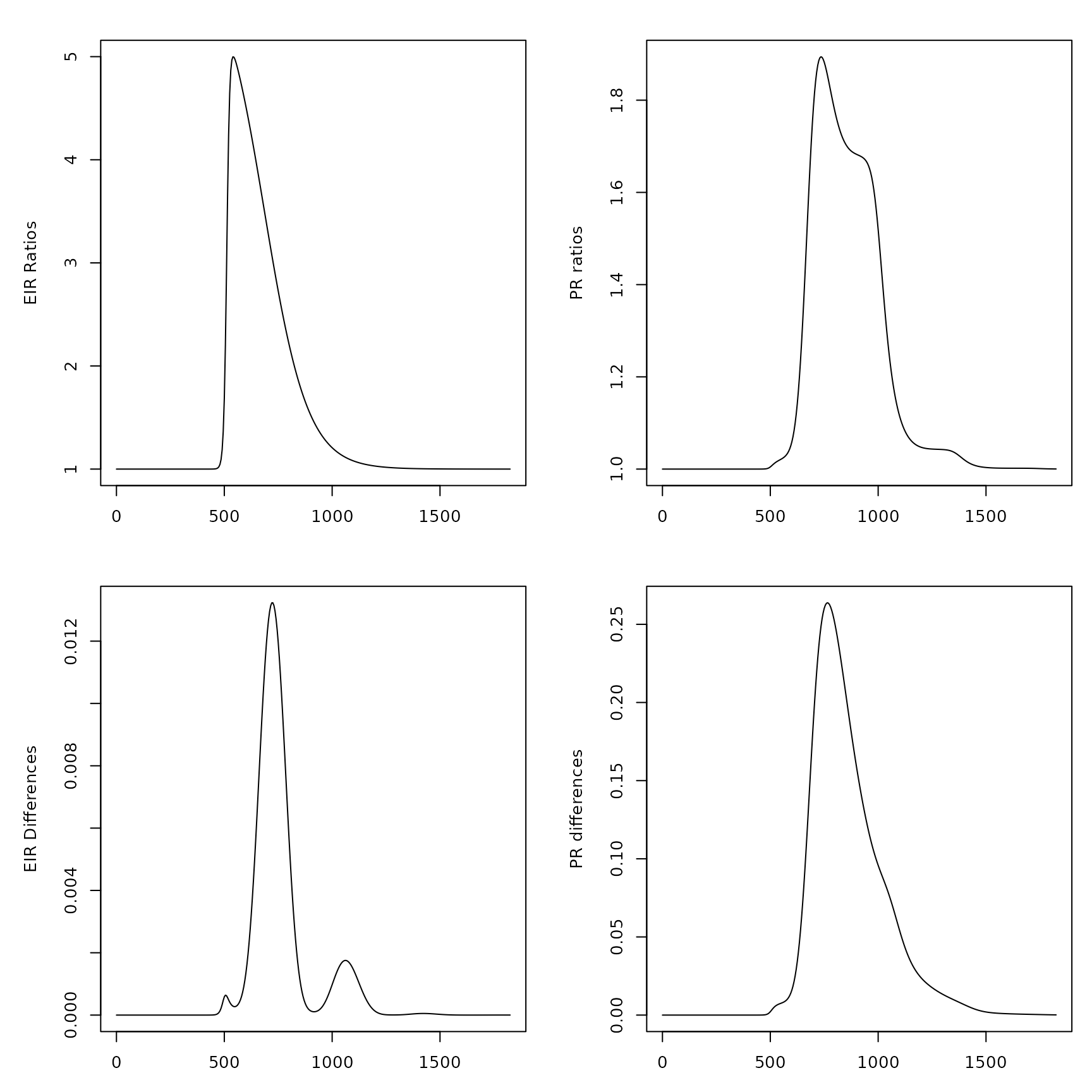
plot(tt, eir1/eir2, type = "l", ylab = "EIR Ratios")
plot(tt, eir1-eir2, type = "l", ylab = "EIR Differences")
plot(tt, pr1/pr2, type = "l", ylab = "PR ratios")
plot(tt, pr1-pr2, type = "l", ylab = "PR differences")