The adult mosquito model RMG
A Behavioral State Model
February 12, 2024
Source:vignettes/MYZmod-RMG.Rmd
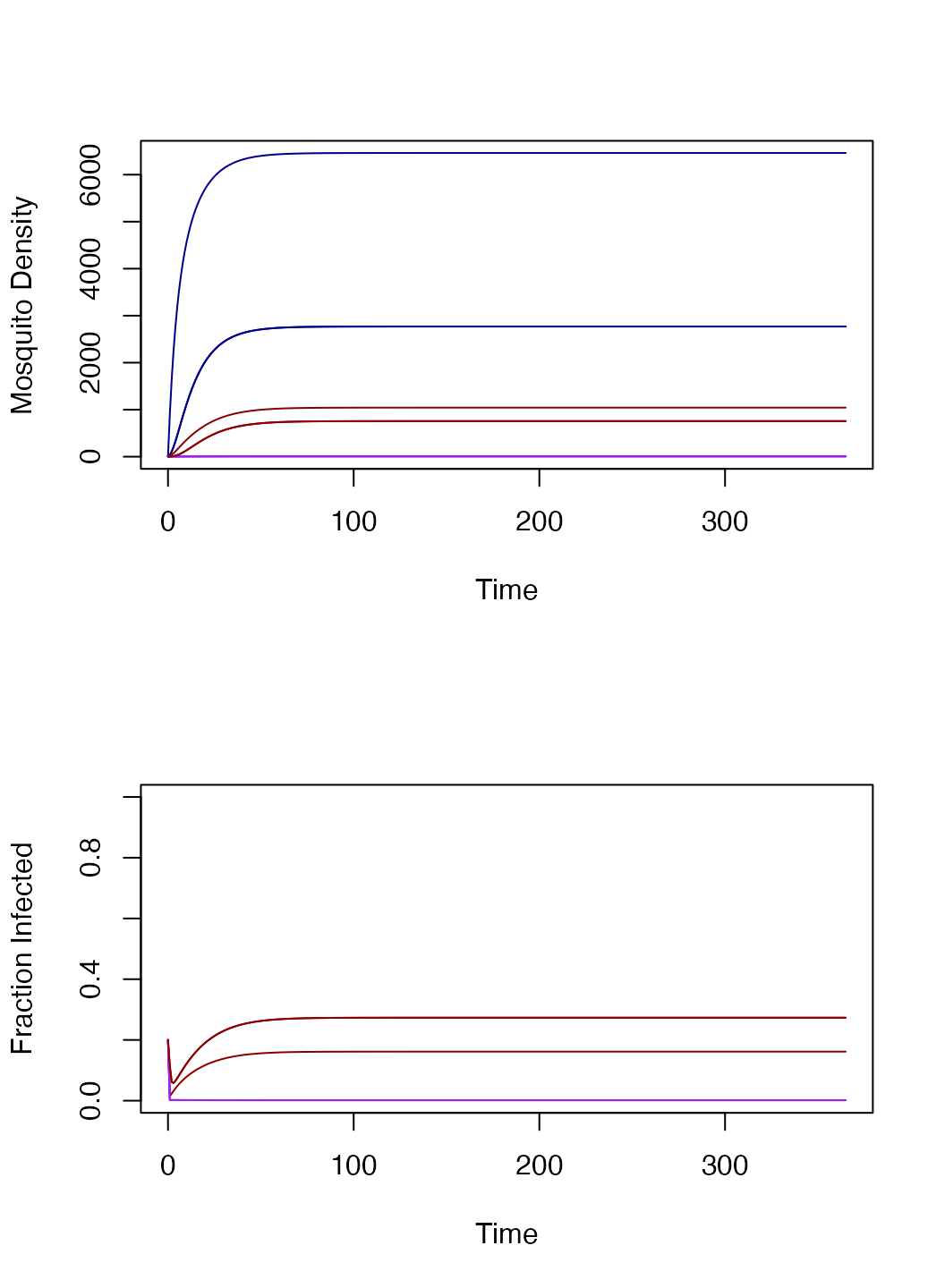
MYZmod-RMG.RmdMost of the models developed to model malaria parasite infections in mosquitoes look at the infection states: uninfected; infected; or infected and infectious. A few models have been developed that track also track parity. A different class of models tracks the behavioral / physiological state of mosquitoes, so we call them behavioral state models. A model with both infection states and behavioral states was first published by Le Menach, et al. (2005)1.
The Model
This is a patch-based model with \(p\) patches, and we assume that all the parameters, variables, and terms are of length \(p\) except for \(\Omega_b\) and \(\Omega_q\), which are \(p \times p\) matrices.
Variables
\(U_b\) - uninfected, blood feeding mosquitoes
\(U_q\) - uninfected, egg laying mosquitoes
\(Y_b\) - infected but not infective, blood feeding mosquitoes
\(Y_q\) - infected but not infective, egg laying mosquitoes
\(Z_b\) - infective, blood feeding mosquitoes
\(Z_q\) - infective, egg laying mosquitoes
Terms
Two terms are passed from another component of the model.
\(\Lambda\) - the emergence rate of adult mosquitoes from aquatic habitats in each patch
\(\kappa\) - the net infectiousness of humans, the probability a mosquito becomes infected after blood feeding on a human
Parameters
Bionomics - Each one of the following parameters can take on a unique value in each patch.
\(f\) - the blood feeding rate
\(q\) - the human blood feeding fraction
\(\nu\) - the egg laying rate
\(g\) - the mosquito death rate, per mosquito
\(\varphi\) - the rate that infected mosquitoes become infective, the inverse of the EIP
\(\sigma_b\) - the patch emigration rate for blood-feeding mosquitoes
\(\sigma_q\) - the patch emigration rate for egg-laying mosquitoes
Dipsersal Matrices - Each one of the following parameters can take on a unique value in each patch.
\({\cal K}_b\) - the dispersal matrix for blood-feeding mosquitoes, which has the form: \[{\cal K} = \left[ \begin{array}{ccccl} 0 & k_{1,2} & k_{1,3} & \ldots & k_{1,p} \\ k_{2,1} & 0 & k_{2,3} & \ldots & k_{2,p} \\ k_{3,1} & k_{3,2} & 0 & \ldots & k_{3,p} \\ \vdots& \vdots &\vdots & \ddots & k_{p-1, p} \\ k_{p,1} & k_{p,2} & k_{p,3} & \ldots & 0 \\ \end{array} \right].\] The diagonal elements are all \(0\), and other elements, \(k_{i,j} \in {\cal K}\), are the fraction of blood feeding mosquitoes leaving patch \(j\) that end up in patch \(i\); the notation should be read as \(i \leftarrow j\), or to \(i\) from \(j\). Notably, the form of \(\cal K\) is constrained such that \[\sum_i k_{i,j} = 1.\]
\({\cal K}_q\) - the dispersal matrix for egg-laying mosquitoes, which has the same form as \({\cal K}_b\)
The Demographic Matrices
\(\Omega_b\) - the demographic matrix for blood feeding mosquitoes; letting \(I\) denote the identity matrix, \[\Omega_b = \mbox{diag}\left(g\right) - \mbox{diag}\left(\sigma_b\right) \left(I - \cal K_b \right)\]
\(\Omega_q\) - the demographic matrix for egg laying mosquitoes; which has the same form as \(\Omega_b\).
Dynamics
The following equations track adult mosquito behavioral and infection dynamics. A key assumption is that a fraction \(q\kappa\) of blood feeding, uninfected mosquitoes become infected, thus transition from \(U_b\) to \(Y_g.\)
\[ \begin{array}{rl} \dfrac{dU_b}{dt} &= \Lambda + \nu U_g - f U_b - \Omega_b \cdot U_b \\ \dfrac{dU_g}{dt} &= f (1- q \kappa) U_b - \nu U_g - \Omega_g \cdot U_g \\ \dfrac{dY_b}{dt} &= \nu Y_g + \phi Y_g - (f+\varphi) Y_g - \Omega_b \cdot Y_b \\ \dfrac{dY_g}{dt} &= f q \kappa U_b + f Y_b - (\nu + \varphi) Y_g - \Omega_g \cdot Y_g \\ \dfrac{dZ_b}{dt} &= \varphi Y_b + \nu Z_g - f Z - \Omega_b \cdot Z_b \\ \dfrac{dZ_g}{dt} &= \varphi Y_g + f Z - \nu Z - \Omega_q \cdot Z_q \end{array} \]