MoI

Comparing Methods

library(ramp.falciparum)
library(deSolve)
library(knitr)

In 1950, George Maccdonald published a model of malaria superinfection (Macdonald G, 1950)¹. He was trying to understand how reexposure would affect the prevalence of infection in a population. In particular, if people are continuously becoming reinfected, then how long would it take until a person would clear all of the parasites to become uninfected again? Macdonald described one model, but the mathematical formula he used in the paper didn’t match his description. (Paul Fine’s essay on the problematic formulation of Macdonald’s model for superinfection is highly recommended reading (Fine PEM, 1975)².)

In 1974, Dietz presented slightly different solution to the problem of clearance with superinfection in a mathematical model developed for the Garki Project (Dietz K, 1974)³; the clearance rate was a function of the force of infection ($h$) and the clearance rate ($r$):

$$\frac{h}{e^{h/r} -1}$$

Dietz’s function was based on a steady state solution to a model from queuing theory, called $M/M/\infty$.

An elegant solution to the problem of superinfection was proposed by Nåsell, who developed a hybrid modeling approach (Nåsell, 1985)⁴. The random variables approach to the problem was formulated by Henry, et al., and this hybrid approach figures prominently in ramp.falciparum.

The following is a demonstration of software in ramp.falciparum. Using the software, we show that all three approaches give identical answers.

Finally, we derive a correct formula for the clearance rate under superinfection.

$M/M/\infty$

The model Macdonald described is called $M/M/\infty$. In this model, each new infection increases the MoI by one; the transition rate to a higher MoI is the force of infection (FoI), denoted $h$. Each parasite can clear at some rate, $r$. The following diagram shows how the fraction of the population with a given MoI, denoted $\zeta_i=i$, changes over time.

---

$$\begin{equation} \begin{array}{ccccccccc} \zeta_0 & {h\atop \longrightarrow} \atop {\longleftarrow \atop r} & \zeta_1 & {h\atop \longrightarrow} \atop {\longleftarrow \atop {2r}} & \zeta_2 & {h \atop \longrightarrow} \atop {\longleftarrow \atop {3r}} & \zeta_3 & {h \atop \longrightarrow} \atop {\longleftarrow \atop {4r}}& \ldots \end{array} \end{equation}$$

---

Changes in the fraction uninfected (MoI=0) are described by:

$$\frac{d \zeta_0}{dt} = r \zeta _1 - h \zeta_0.$$

For those who are infected (with MoI$=i$), the dynamics are:

$$\frac{d \zeta_i}{dt} = h \zeta_{i-1} + r(i+1) \zeta_{i+1} - (r+h) \zeta_i$$ The software in ramp.falciparum includes functions to set up and solve the queuing model $M/M/\infty.$

While $M/M/\infty$ is an infinite system of differential equations, the function solveMMinfinity solves a finite system of differential equations. The maximum MoI is chosen to be large enough that it doesn’t affect the results.

MMinf <- solveMMinfty(5/365, foiP3, Amax=1095)

with(MMinf, plot(time, m, type = "l", ylab = expression(m[tau](a)), xlab = "a - cohort age (in days)"))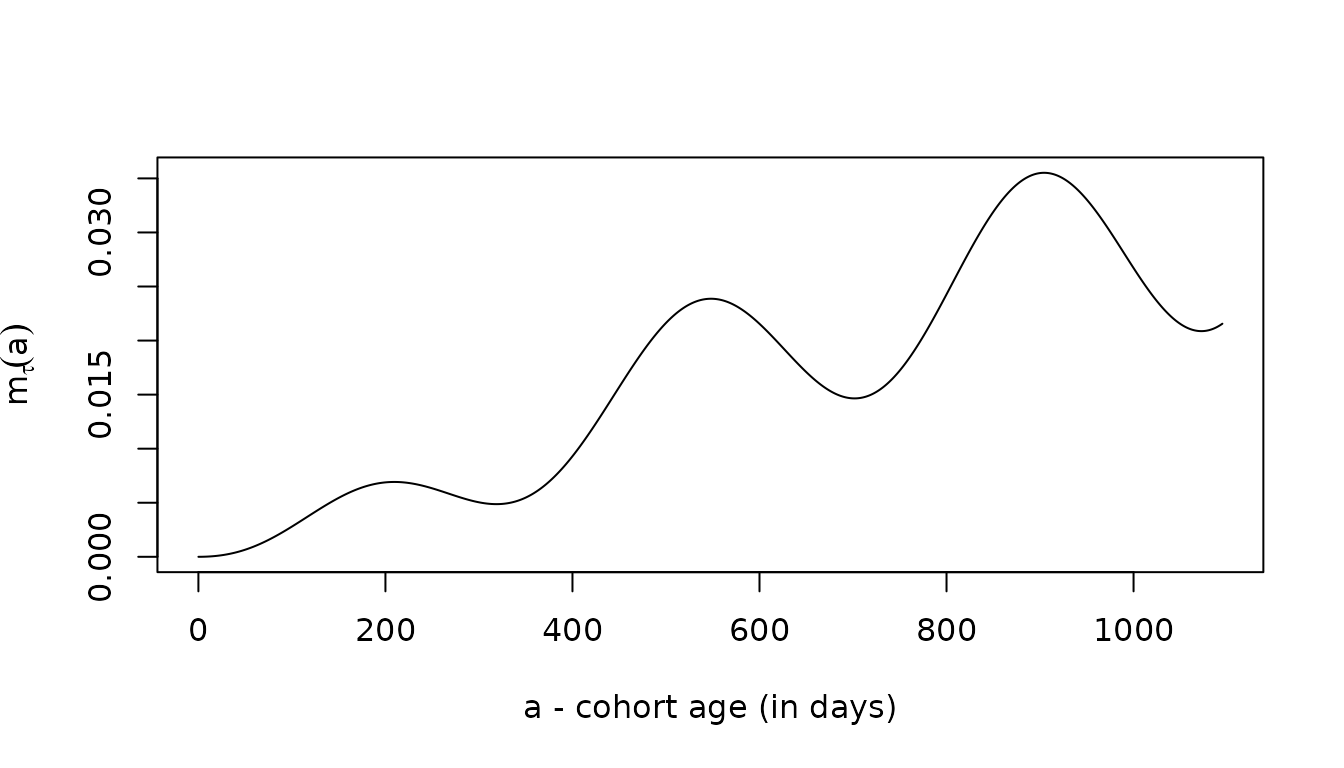

The Hybrid Model

While the infinite system of differential equations can be formulated and solved numerically, Nåsell showed that the system can be described by a simple equation. Let $m$ denote the mean MoI.

$$\frac{dm}{dt} = h-rm$$

He also showed that the distribution of the MoI would converge to a Poisson distribution. If the initial distribution was Poisson, then it would remain Poisson forever.

hybrid = solve_dm(5/365, foiP3, Amax=1095)

with(hybrid, plot(time, m, type = "l", ylab = expression(m[tau](a)), xlab = "a - cohort age (in days)"))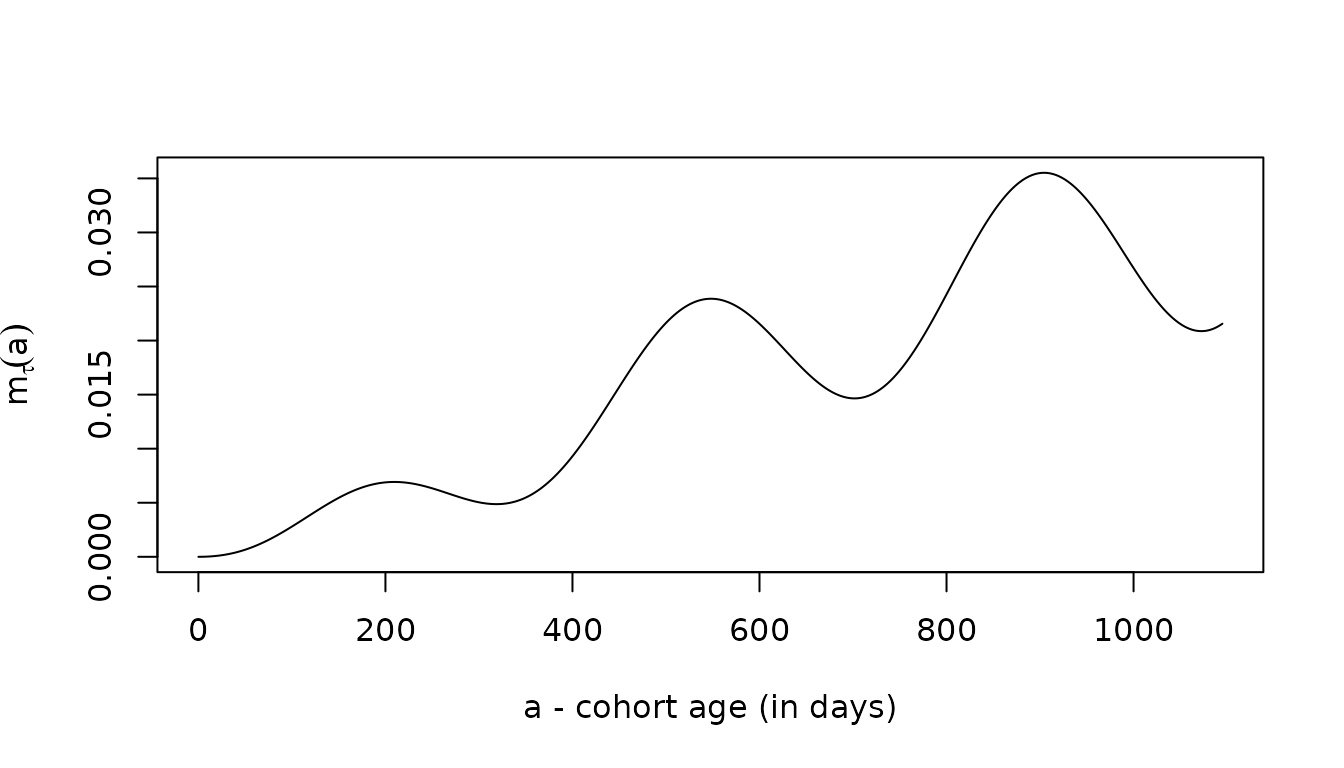

The Random Variables Approach

Let $z(\alpha, a)$ denote the density of parasite cohorts of age $\alpha$ in a host cohort of age $a$. We assume infections clear at the constant rate $r$. Since infections in $M/M/\infty$ are independent, we can track the dynamics for the AoI of all parasite cohorts with the equation,

$$\begin{equation} \frac{\partial z}{\partial a} + \frac{\partial z}{\partial \alpha} = - rz, \end{equation}$$

with the boundary condition $z_\tau(a,0)=h_\tau(a).$ We note that the age of the host birth cohort sets an upper limit for the parasite cohort, so $0 < \alpha < a$. The solution, which describes density of infections of age $\alpha$ in a host cohort of age $a$, is given by the formula:

$$\begin{equation} z_\tau(\alpha, a | h) = h_\tau \left(a-\alpha\right) e^{-r \alpha}. \label{zda} \end{equation}$$

From these equations, we derive random variables describing the MoI, the AoI, and the AoY, noting that the mean MoI is:

$$\begin{equation} m_\tau(a | h) = \int_0^a z_\tau(\alpha, a |h) d \alpha \end{equation}$$

In ramp.falciparum, this is computed with the function meanMoI

moi = meanMoI(aa, foiP3, hhat=5/365)

plot(aa, moi, type = "l", ylab = expression(m[tau](a)), xlab = "a - cohort age (in days)")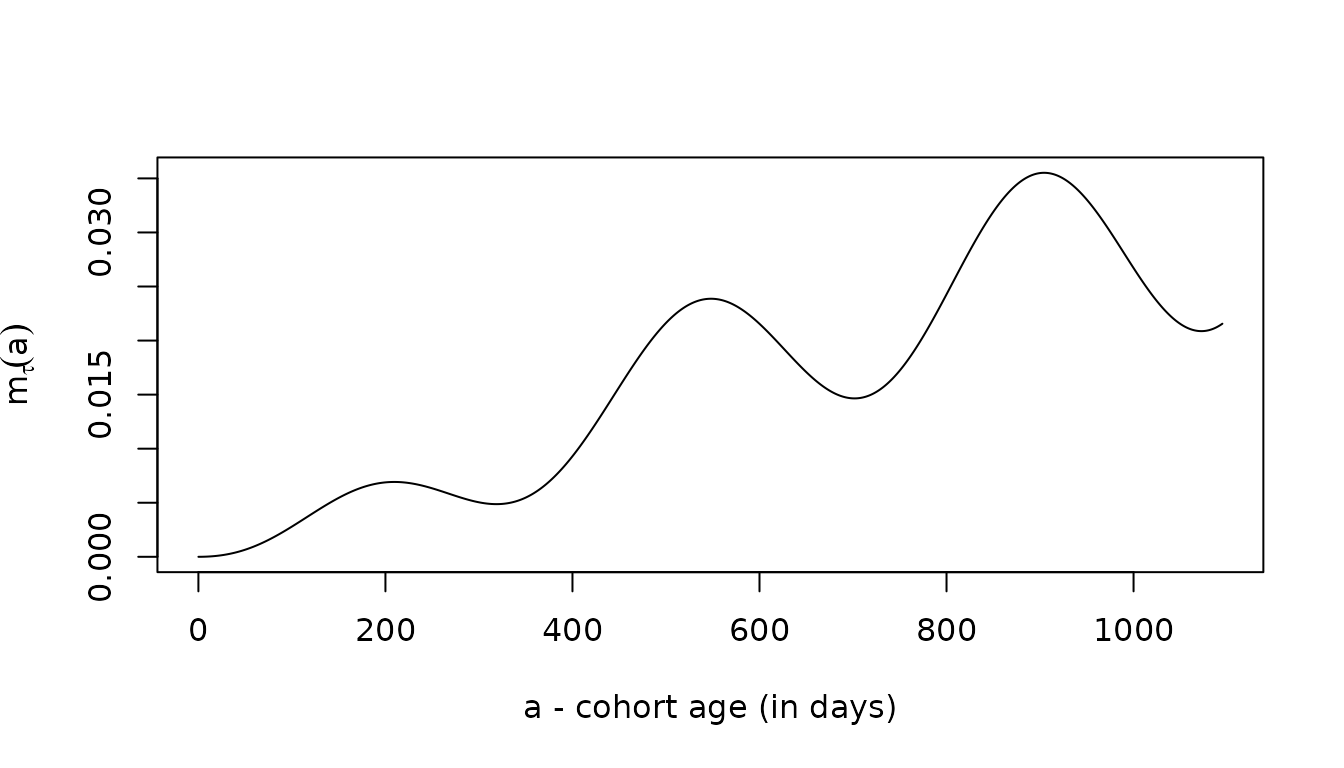

The three give the same answers, up to slight differences introduced by the numerical methods:

c(mean(abs(moi - hybrid$m)) < 1e-9,
mean(abs(MMinf$m- hybrid$m)) < 1e-10,
max(abs(moi - hybrid$m)) < 1e-8,
max(abs(MMinf$m- hybrid$m))< 1e-10)

## [1] TRUE TRUE TRUE TRUE

Prevalence

With all this information at hand, we are now in a position to formulate a model for superinfection.

We note that since $m$ is the mean of a Poisson, the prevalence of infection can be computed directly from $m$. It is the complement of the zero term from a Poisson:

$$p(t) = 1-\mbox{Pois}(\zeta =0; m(t)) = 1 - e^{-m(t)}$$

It is, nevertheless, sometimes useful to know the clearance rate, a transition from MoI = 1 to MoI=0. Clearance from the infected class can only occur if a person is infected with an MoI of one, and if that infection clears:

$$R(m) = r \frac{\mbox{Pr}(\zeta=1; m(t))}{\mbox{Pr}(\zeta>0; m(t))} = r \frac{m e^{-m}}{1-e^{-m}} = r \frac{m}{e^{-m}-1}$$

The change in prevalence is thus described by the equation:

$$\frac{dp}{dt} = h(1-p)-R(m)p$$

While this is interesting, and while it solves the problem of modeling clearance under superinfection, the equation depends on $m$. Since we can compute $p(t)$ directly from $m(t)$, the equation for prevalence is completely redundant.

On the other hand, if we wanted a model for prevalence that did not use $m$, we could rewrite the equation:

$$\frac{dp}{dt} = h(1-p) + r \ln (1-p) \frac{(1-p) }{p}$$

References

---

1. Macdonald G. The analysis of infection rates in diseases in which superinfection occurs. Trop Dis Bull. 1950;47: 907–915↩︎

2. Fine PEM. Superinfection - a problem in formulating a problem. Tropical Diseases Bulletin. 1975;75: 475–488↩︎

3. Dietz K, Molineaux L, Thomas A. A malaria model tested in the African savannah. Bull World Health Organ. 1974;50: 347–357↩︎

4. Nåsell I. Hybrid Models of Tropical Infections. 1st edition. Berlin: Springer-Verlag; 1985. https://doi.org/10.1007/978-3-662-01609-1↩︎